我发现其实前几篇的符号是不甚严谨的，从此片开始，统一将图模型记作花体，节点集合和边集合记为和，而单个节点使用大写字母表示，如.

1 图模型和概率分布

通过上一篇的讨论，可见两个变量之间是否统计相关和所属图模型的结构是分不开的。接下来将对图模型结构和变量概率分布进行讨论。首先引入几个定义：

定义
假设图模型的节点变量集合为，概率分布中的变量集合为。中的所有节点与中的所有变量一一对应。对于中的所有非邻接节点子集（相应对应概率分布变量集合中的，分别简记为）

  1. 如果则称是概率分布的 独立图（Independency Map, I-Map）
  2. 如果 则称是概率分布的 依赖图（Dependency Map, D-Map）
  3. 如果上面两条均满足，则称是的 完美图（Perfect Map, P-map），也称与 同构（Isomorphic） 或 相互忠实（Faithful）。如果分布与某个DAG相互忠实，我们称该分布具有忠实性。

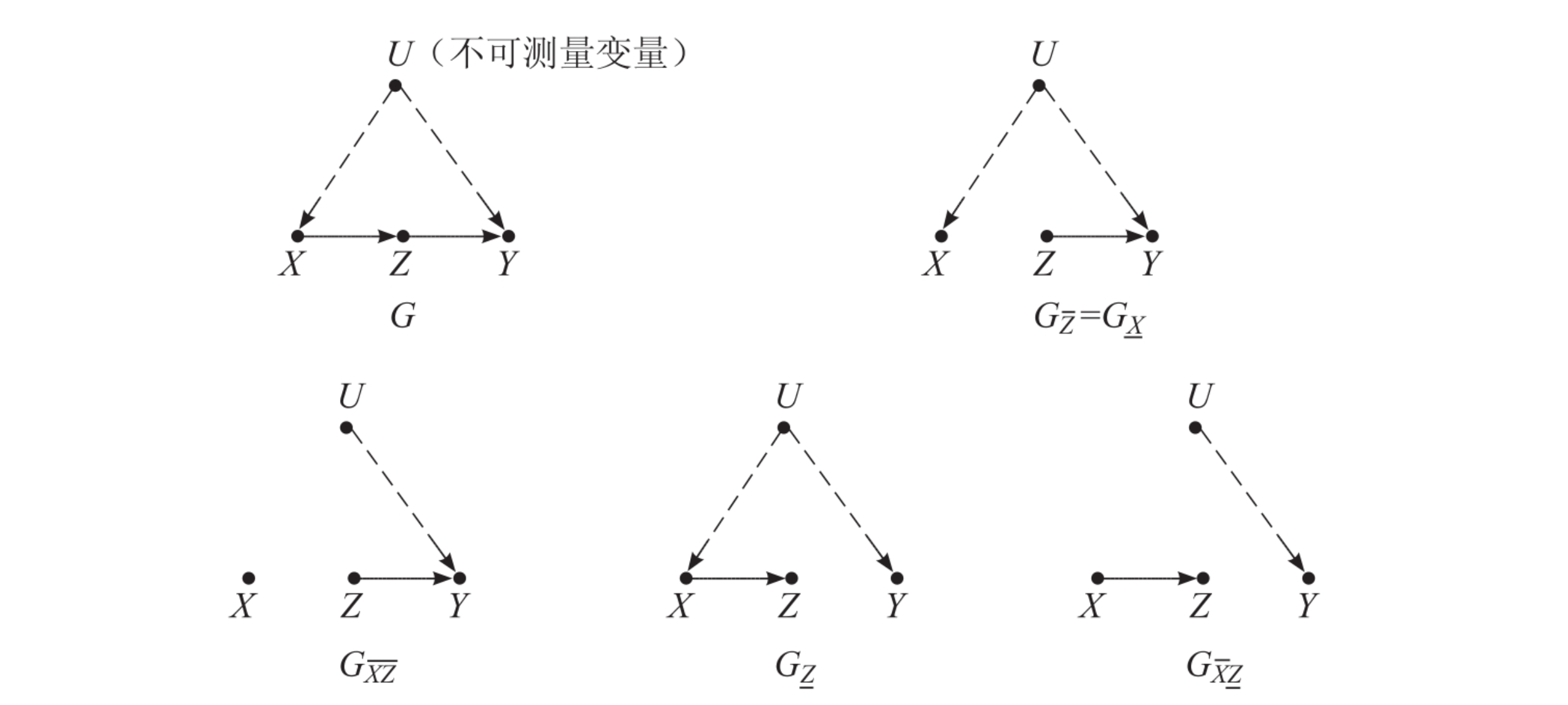
为了理解上述定义，现举分叉结构和链式结构为例，如下图所示：

Pasted image 20240313200414

图1：链式结构（左）和分叉结构（右）

对于链式结构，有；对于分叉结构，有。注意，因此二者相等。像这样图结构不同，但联合概率分布相同的结构，称为是Markov等价（Markov Equivalent）的。

等价关系是一种特殊地关系。一个非空集合上的等价关系是的子集，具有下列性质：

  1. 自反性：，,
    2.传递性：，,
    3.对称性：，.
    可以看到，集合上的一个这样的等价关系会将集合划分成若干等价类（Equivalent Class）。例如所有与元素等价的元素构成集合。

根据等价关系的性质，可以将图模型划分为若干等价类，它们常被表示为完全部分有向的无环图（Completed Partially Directed Acuclic Graph，CPDAG），相关研究发现，真正影响概率分布的边（有些边不影响概率分布，其朝向也就无关紧要了）至少在图模型中属于至少一个“V结构”（对撞结构）。因此在CPDAG中，只有V结构中的边或环（确定边，Compelled Edges）才具有方向。

定义（Markov毯，Markov Blanket）
对于图模型，针对其节点变量中的任意节点，满足条件的最小子集，称为节点的Markov毯。

定理
对于具有Markov性的有向无环图，其节点的Markov毯即为其父节点、子节点和与共子节点的其他节点的并集。例如在下图中，节点的Markov毯为：

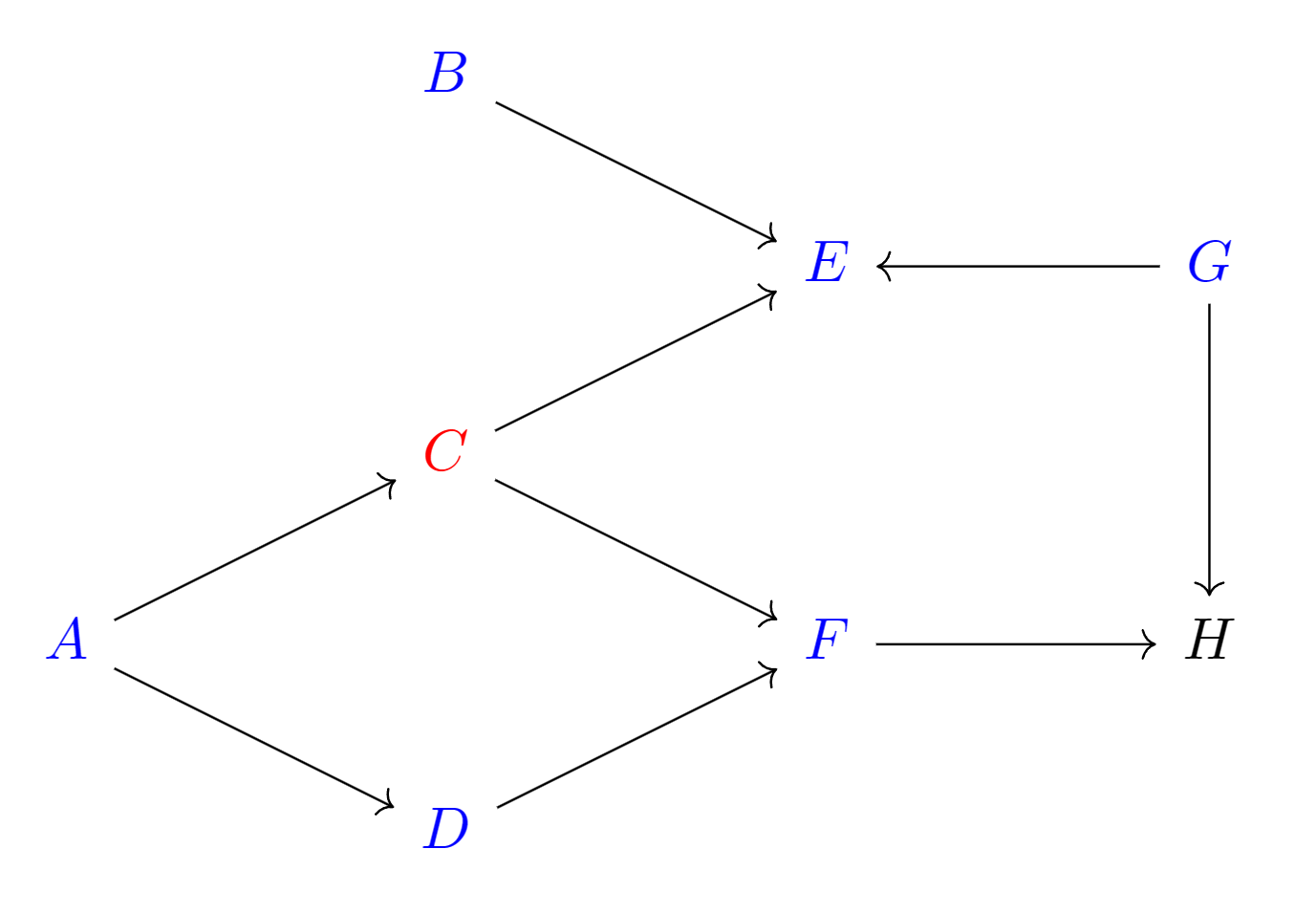
Pasted image 20240315202445

图2：一个Markov图。节点C（红色）及其Markov毯（蓝色）
  1. 有向无环图的条件：
    有向无环图中，是的任意子集，记为节点集合的所有父母节点组成的集合，为集合所有后代节点组成的集合。在给定的条件下，节点变量集合独立于中的所有非后代节点（不含父母节点），则称具有Markov性。
  2. 因果模型对应的有向无环图满足Markov性。因为给定节点，固定其父节点后，满足Markov性（见前一篇）。

为了进一步介绍Markov等价，需要引入“框架”的概念。一个有向图的 框架（Skeleton） 就是将其有向边全部变成无向边得到的无向图：

定义（框架，Skeleton）
对于一个DAG，若将其边集进行拓展，得到​，也即有向边的方向被抹去，就得到了这个图的框架，如下图所示：

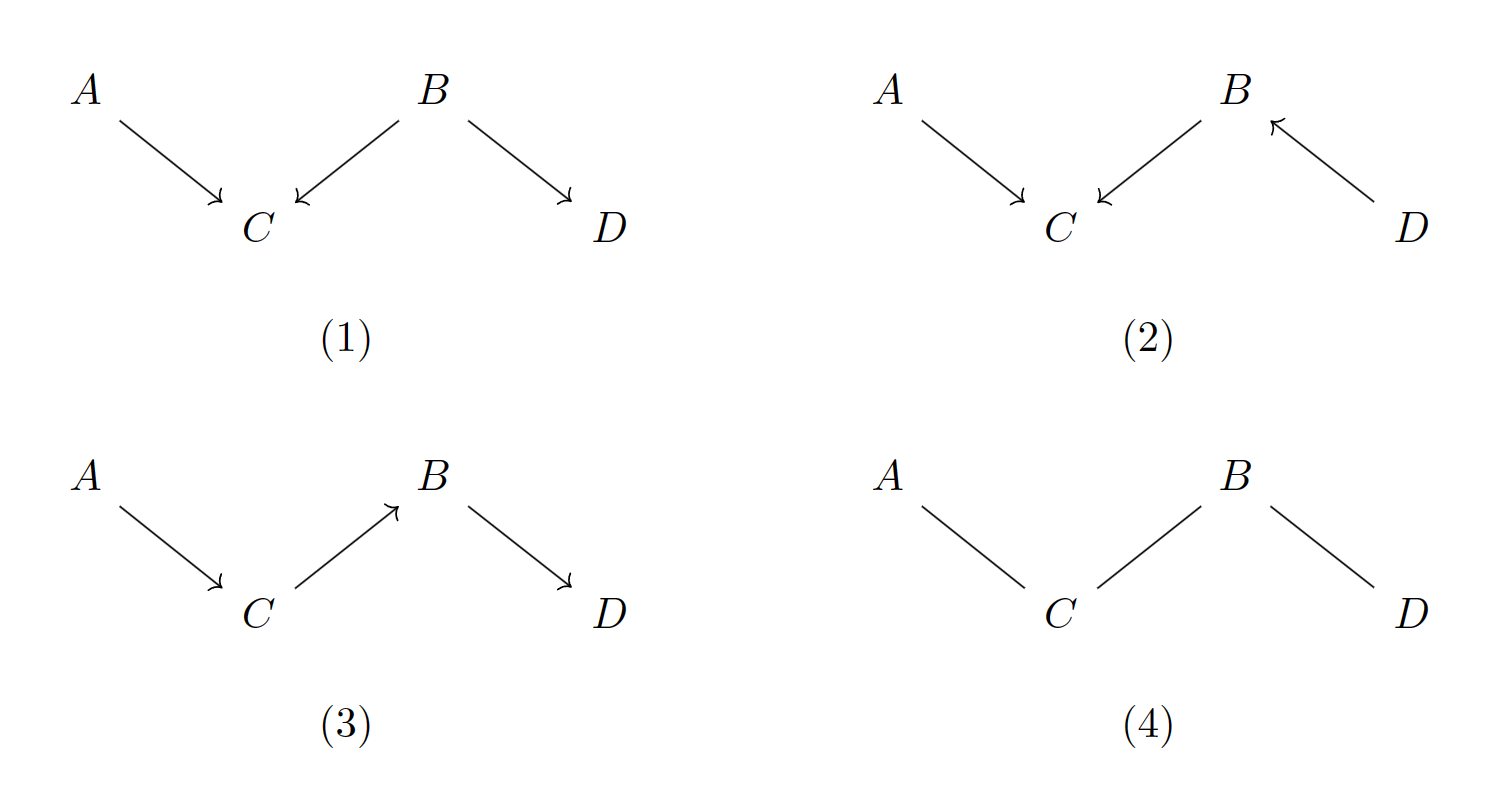
Pasted image 20240315210648

图3：图(1)，(2)，(3)的框架相同，都是(4)

定理
如果两个图模型的框架相同，且所有V结构相同（是否可以置换为所有对撞结构数量和位置都相同），则这两个图Markov等价。

为了更加直观的表示，请看下面几个例子：

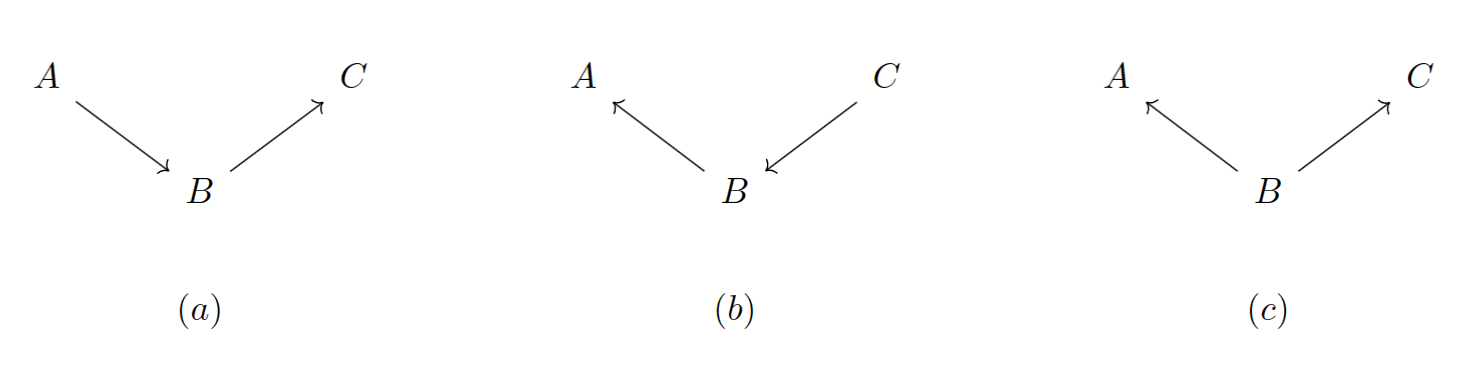
Pasted image 20240315211009

图4：三个图中没有对撞结构，框架相同，所以Markov等价

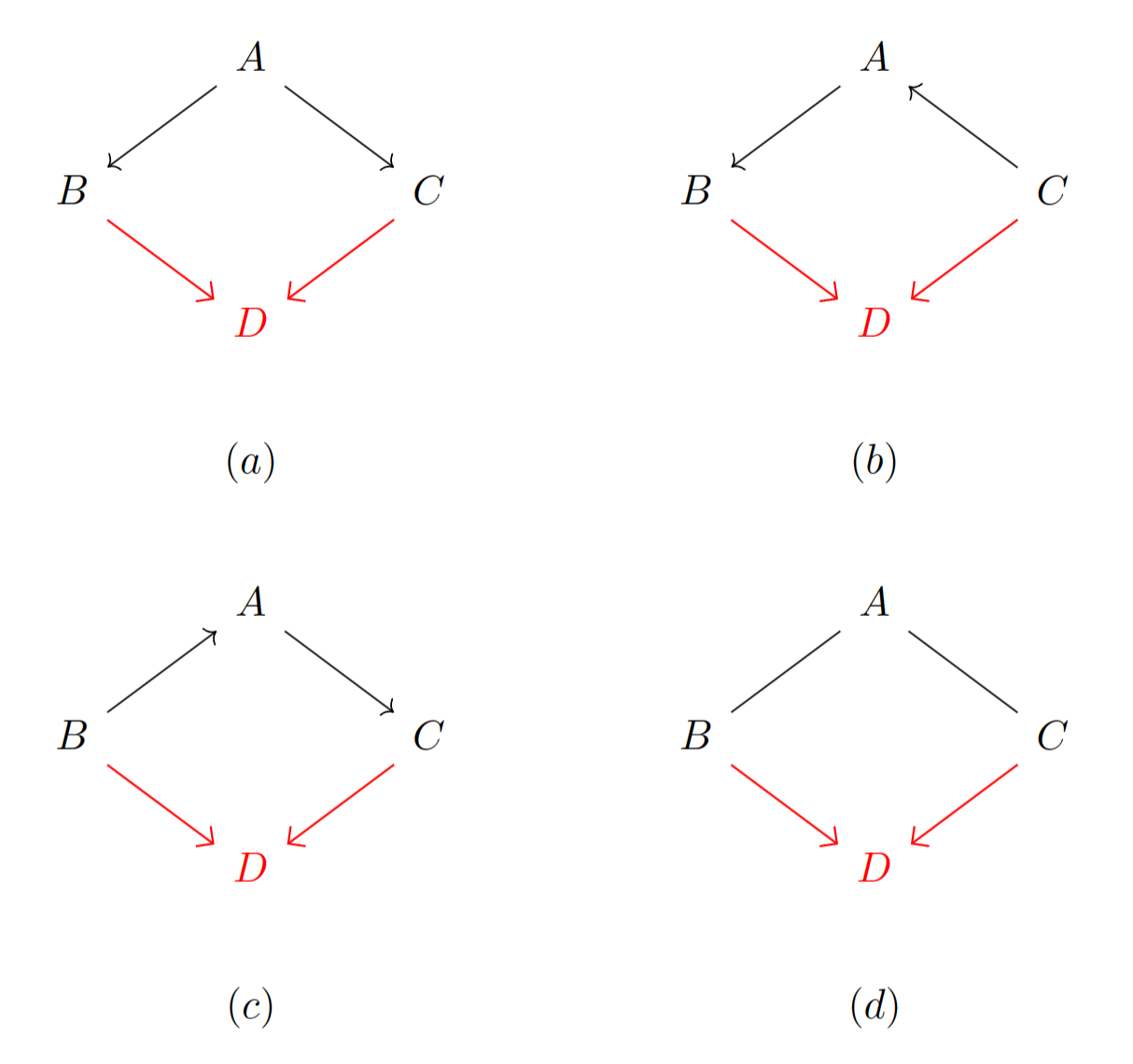
Pasted image 20240315212716

图5：图(a)，(b)和(c)的框架是(d)；且这三个图Markov等价

2 图模型分析的编程实现

2.1 图模型分析的R实现

使用R中的DAGitty包构建下面的图模型：

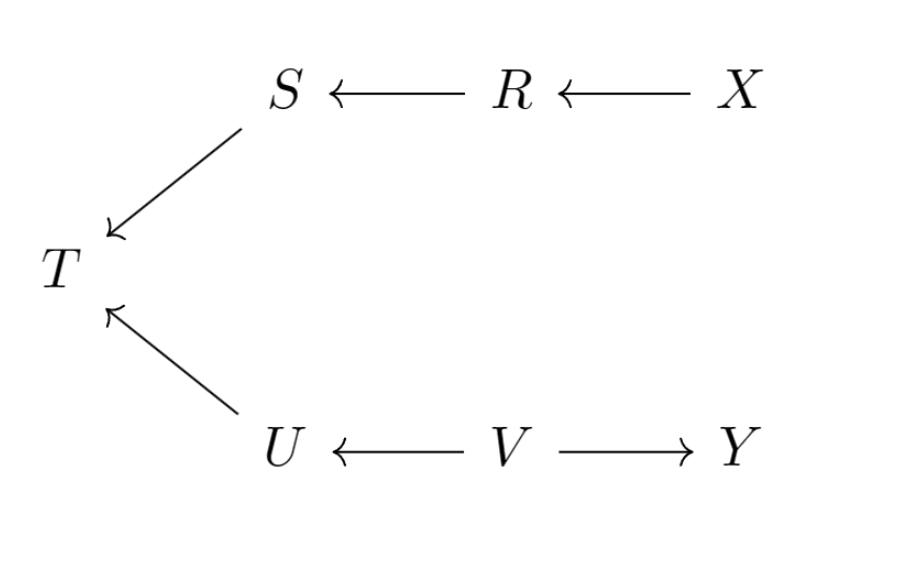
Pasted image 20240315213508

图6：图模型G1
> library('dagitty')
> g1 <- dagitty("dag {
      X -> R -> S -> T <- U <- V -> Y
      }")

Pasted image 20240315213938

图7：图模型G2
> g2 <- dagitty("dag {
      X -> R -> S -> T <- U <- V -> Y
      T -> P
      }")

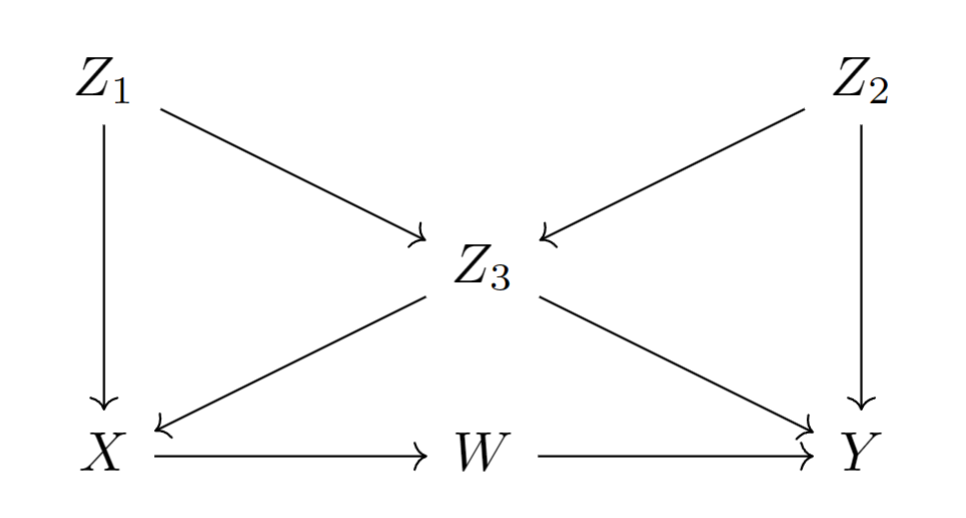
Pasted image 20240315214129

图8：图模型G3
> g3 <- dagitty("dag {
      X <- Z_1 -> Z_3 <- Z_2 -> Y
      X <- Z_3 -> Y
      X -> W -> Y
      }")
> coordinates(g3) <- list(
      x=c(X=1, W=2, Y=3, Z_1=1, Z_3=2, Z_2=3),
      y=c(X=0, W=0, Y=0, Z_1=-2, Z_3=-1, Z_2=-2)
      )

下面介绍一些常用的函数：

1. 路径函数paths()
函数的签名如下：

paths(g,                   # 图模型
      from=exposures(x),   # 起点
      to=outcomes(x),      # 终点
      z=list(),            # 路径中需要控制的节点集合，默认为空集
      limit=100,           # 限制路径中的节点数量
      directed=FALSE
      ) 
-> 
$$paths,   # 符合要求的所有路径
$$open     # 对应的路径是否被阻断

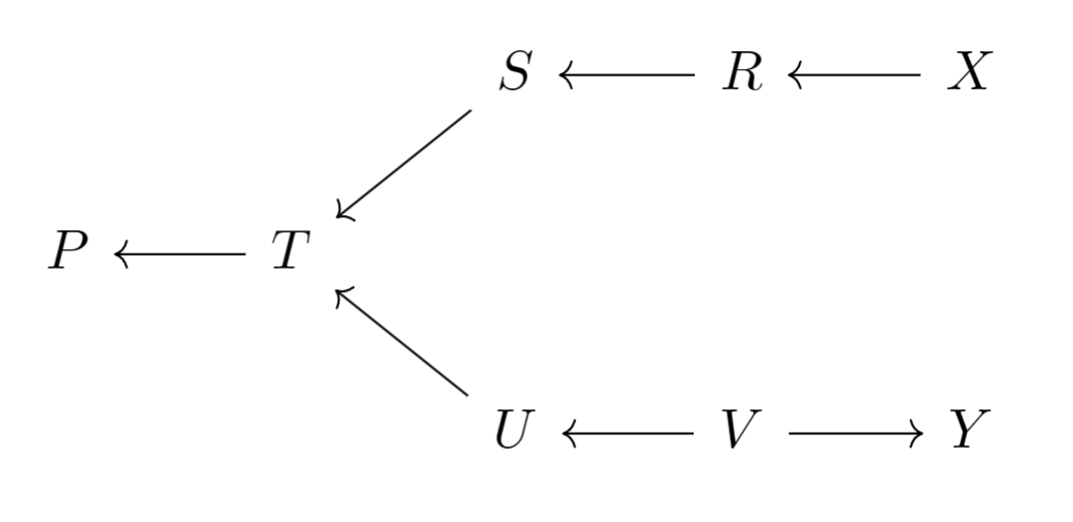
例如，在图模型中，考察在给定时从到有无联通路径：

paths(g1, "X", "Y", c("R", "V"))
# 输出结果
# $$paths
# [1] "X -> R -> S -> T <- U <- V -> Y"
# $$open
# [1] FALSE

可见，在给定条件下，没有未被阻断的路径。进一步地，可以编写函数判断中的任意两个节点在给定时是否相互独立。

为了防止读者忘记，的结构如下：

pairs <- combn(c("X", "S", "T", "U", "Y"), 2)
apply(pairs,
      2, 
      function(x){
          p <- paths(g1, x[1], x[2], c("R", "V"))
          if(!p$$open){ message(x[1], " and ", x[2], " are independent given {R,V}") }
          else{ message(x[1], " and ", x[2], " are possibaly dependent given {R,V}") }
        }
      )
# 输出结果：
# X and S are independent given {R,V}
# X and T are independent given {R,V}
# X and U are independent given {R,V}
# X and Y are independent given {R,V}
# S and T are possibaly dependent given {R,V}
# S and U are independent given {R,V}
# S and Y are independent given {R,V}
# T and U are possibaly dependent given {R,V}
# T and Y are independent given {R,V}
# U and Y are independent given {R,V}
# NULL

在上面的代码中，

  • combn()函数将参数中的元素凉凉组合，并赋值给数组pairs
  • apply()函数将函数function(x)作用在pairs中的每个元素中
  • if(!p$$open)判断该路径是否被阻断，如果两点之间有多条路径，则需要对此进行修改

2. impliedConditionalIndependencies()
函数接受一个图为参数，输出图中所有节点的条件独立性关系：

impliedConditionalIndependencies(g3)
# 输出结果
# W _||_ Z_1 | X
# W _||_ Z_2 | Z_1, Z_3
# W _||_ Z_2 | X
# W _||_ Z_3 | X
# X _||_ Y | W, Z_2, Z_3
# X _||_ Y | W, Z_1, Z_3
# X _||_ Z_2 | Z_1, Z_3
# Y _||_ Z_1 | X, Z_2, Z_3
# Y _||_ Z_1 | W, Z_2, Z_3
# Z_1 _||_ Z_2

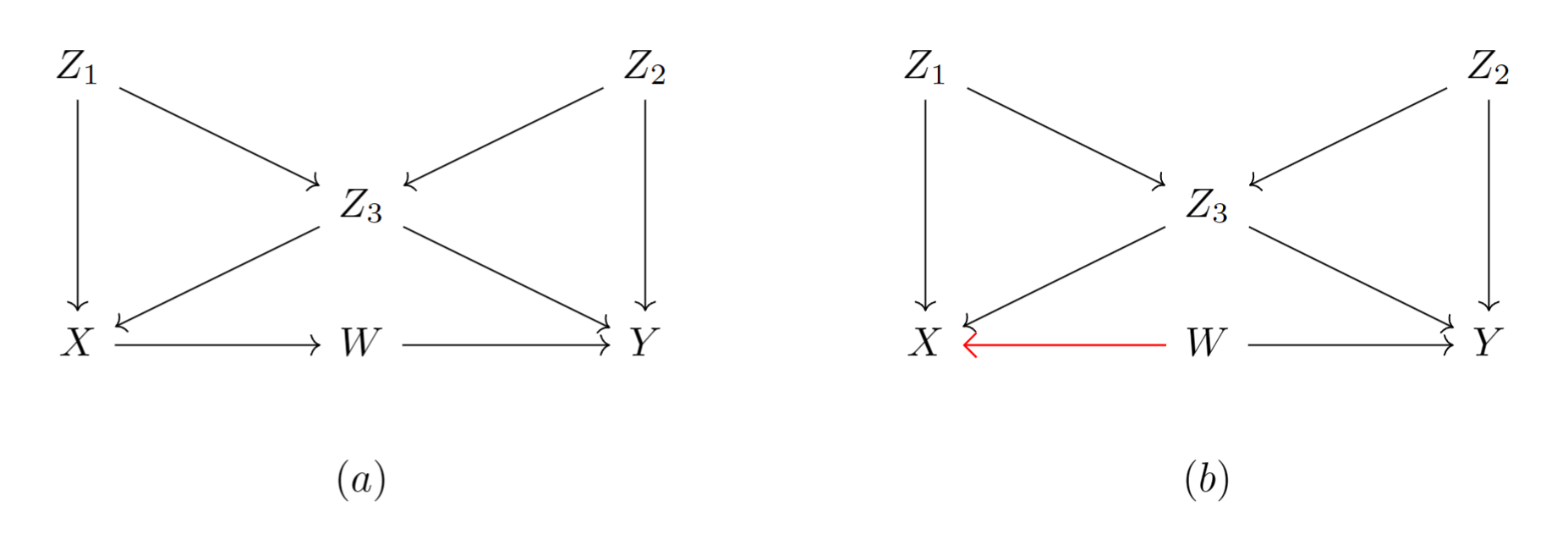
进一步地，可以对图模型设置可观测的节点。例如对设置可观测节点为（其他不可观察），然后求其中所有非相邻节点的独立性关系：

latents(g3) <- setdiff(names(g3), c("Z_3", "W", "X", "Z_1"))
impliedConditionalIndependencies(g3)
# 输出结果
# W _||_ Z_1 | X
# W _||_ Z_3 | X

其中setdiff()函数求得图模型中除了给出参数以外的所有其他节点。

3. dseparated()和dconnected()
这两个函数求图中的两个节点集合和是否被节点集合所d-划分。它们的签名如下：

dseparated(g, X, Y, Z)
dconnected(g, X, Y, Z)
  • 当都不为空集时，返回bool值：是否将和d-划分或d-连通
  • 当为空集时，返回值为在给定的条件下与d-连通或被d-划分的所有结点

回忆d-划分的定义，两个节点集合被第三个节点集合所d-划分，表示在给定第三个集合时，前两个集合中每个任取一个节点，它们之间的通路都被阻断。

4. markovBlancket()
函数的签名如下：

markovBlanket(g, v)

其中g为输入的图模型，v为节点，类型为字符串。函数接收这两个参数，输出的Markov毯的所有节点。

5. equivalenceClass()和equivalentDAGs()

两个函数都接受一个参数，即图模型，前者输出这个图对应的等价类，后者输出等价类中所有和输入的图模型等价的图模型，例如

equivalenceClass(g3) 
equivalentDAGs(g3)
# 与它等价的图模型只有它本身

这里需要稍微动动脑筋。假设将这条有向边倒转，则形成了对撞结构（如下图所示），因此该图模型的等价类就是它自己构成的集合。

Pasted image 20240315231108

图9：如果将X到W的边倒转（红色），则会出现新的对撞结构

2.2 图模型分析的Python实现

TODO