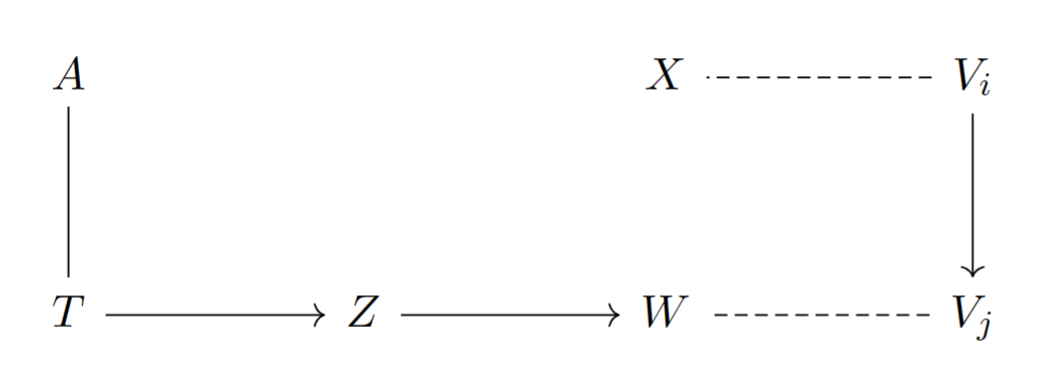【基于图模型的因果推断】4 图模型的分析
1 基本图模型结构的分析
1.1 入室盗窃还是热带风暴
Holmes先生在办公室接到邻居打来的电话,邻居告诉他:他家的防盗警报响了。由于担心家中被盗,Holmes先生立刻开车回家。在回家的路上,Holmes先生在广播中听说他家一带正在发生热带风暴。考虑到可能是风暴误触发了防盗警报,他又驾车返回公司。
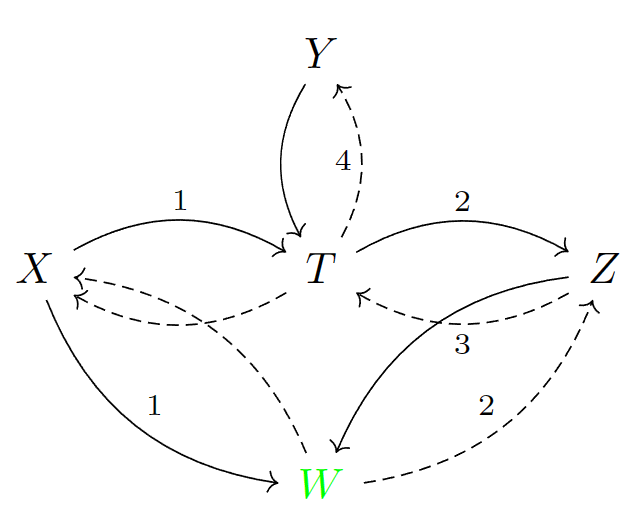
那么核心问题是,到底是什么(以多大的概率)触发了防盗警报?根据提供的信息,我们可以画出这个问题对应的因果图。其中表示Holmes先生家中是否被盗,表示是否发生热带风暴,表示警报是否响起,表示电台是否告知发生热带风暴。这几个变量都是二值变量:代表发生,代表不发生
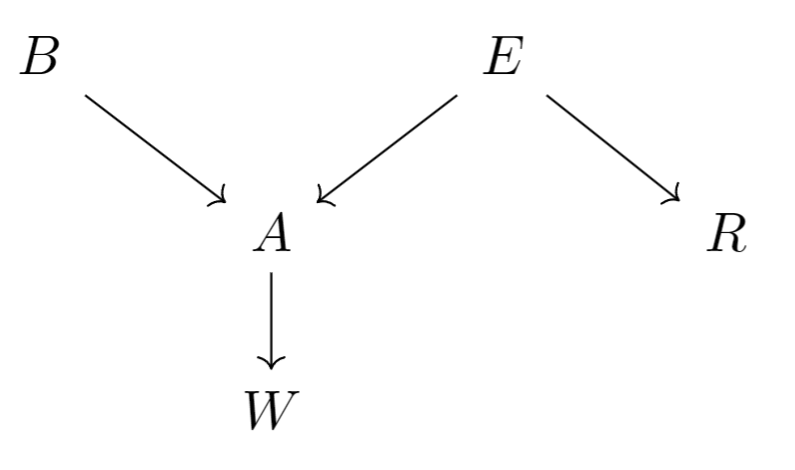
不难注意,在图中采样路径的时候会遇到下面三种结构:
| 结构名称 | 结构图示 |
|---|---|
| 链 | |
| 分叉 | |
| 对撞 |
事实上,这是组成任何图模型结构的基本结构。下面将着重讨论这三种基本结构。
1.2 链
在图1中,我们取路径进行分析,具体分为固定和不固定两种情况。
不固定
不固定的情况下,它会受到的影响:如果,那么大概率会等于。在这种情况下,邻居可以通过观察来决定。换句话说,会受到的影响。反过来说,如果,则一定概率下可以推知。总之,在链式结构中,没有给定中间变量取值的条件下,两端的节点变量会互相影响(如下图所示).
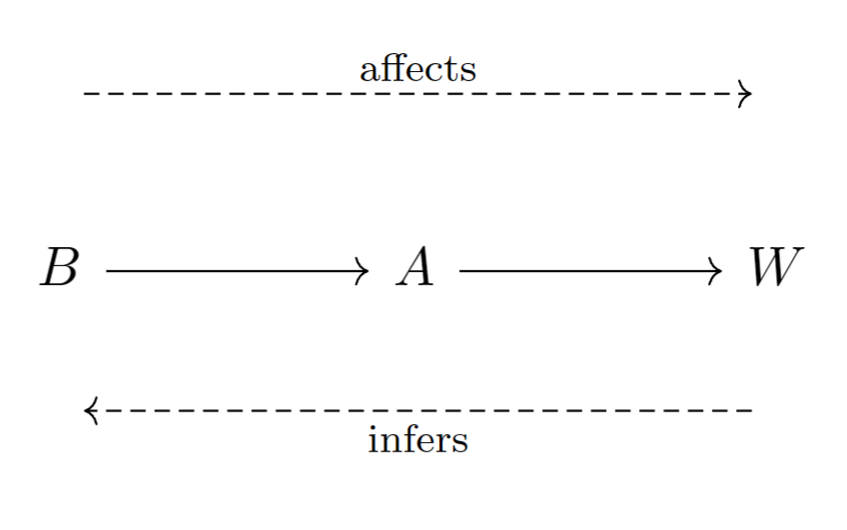
固定
如果控制了中间的节点,事情就变得不同了。试想如果由某些外力使得,以及这两条信息通道将会被阻断。如果报警机构出现故障,此时相当于被固定为一个值,它就不能反映家中是否失窃,同时通过邻居的反映也无法得知此事。总之,在链式结构中,如果中间变量被固定为某个值,则两端节点之间的信息通道将会被截断(如下图所示).
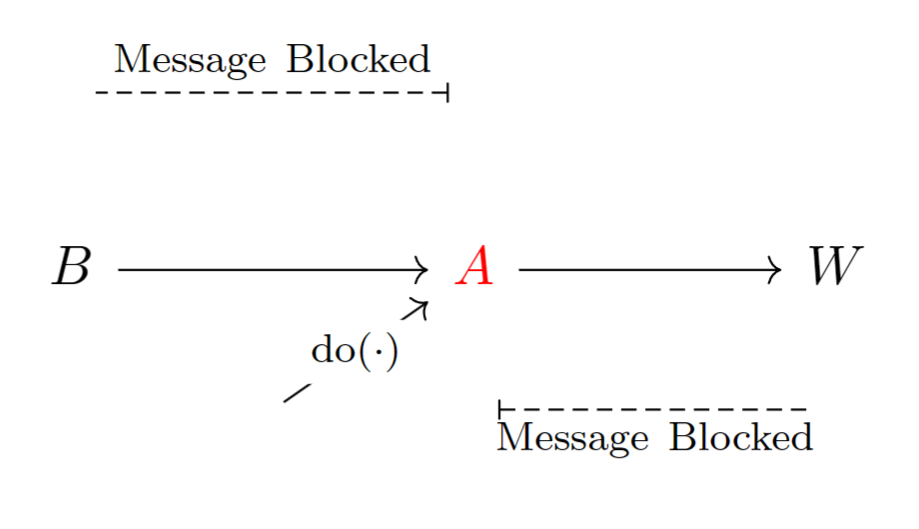
联合概率
从数学的角度,也可以这样考虑。在图2和图3所示的因果图中,所有变量的联合分布有
将展开,整理得
于是得到,这也印证了上面做两种分类的意义。
在考虑作为随机变量的变量时,我们为了简便使用大写(上一篇中用的是正体,是为了和其他进行区分)。当考虑变量取某个值的概率时,我们用小写。
1.3 分叉
下面以图1中的分叉结构作为例子进行讨论。类似地,我们也做中间变量固定与否的两种情形。
为了防止读者忘记这些符号的含义,这里做一下Reminder:是报警是否启动,是热带风暴是否发生,是电台是否广播发生热带风暴。
不固定
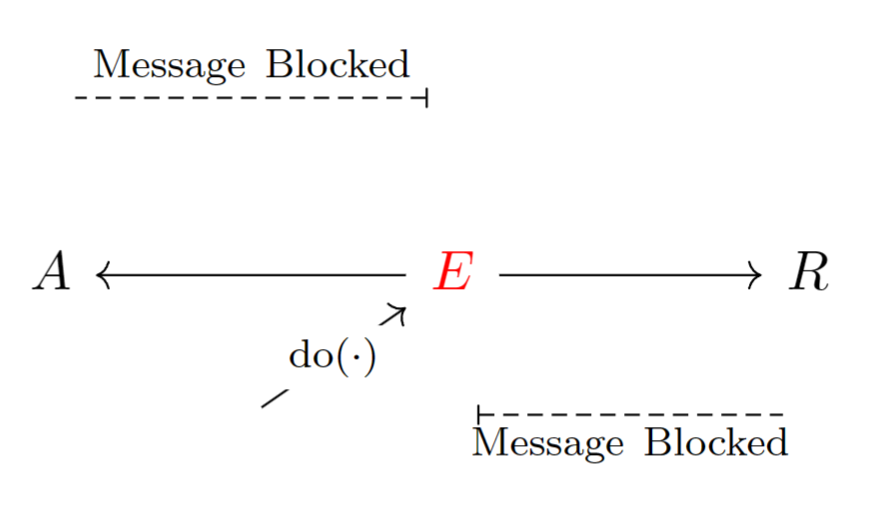
有了上面的一个例子,我想我们现在已经轻车熟路了。在不固定中间节点的情况下,的情形下很可能造成且。于是如果观测到,那么很可能我们也可以观测到。总之,分叉结构中的中间变量不被固定时,两侧变量可以相互影响,如下图所示。
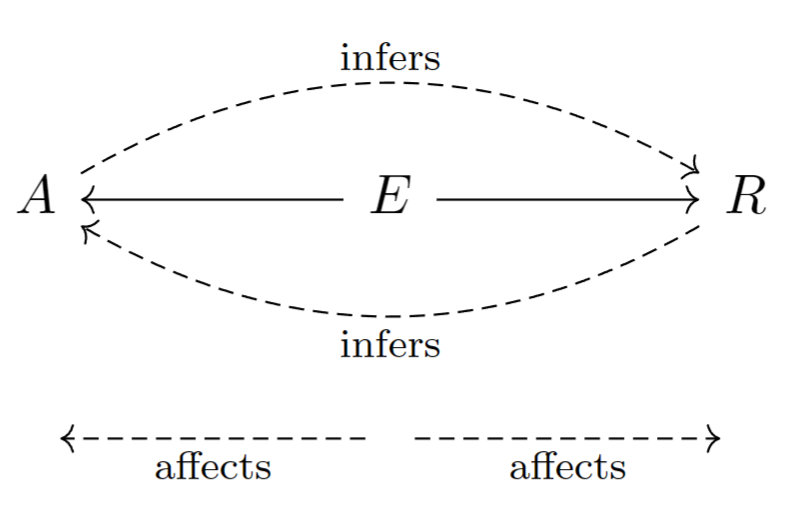
固定
反过来,一旦被固定,无论的值如何变化,都不会影响到。(因为在本例中,二者没有其他的共因)。十分类似地,路径两端变量之间的信息传递将再次被阻断,如下图所示。
联合概率
我们再来考虑这个小系统中变量的联合概率:
然后考虑条件概率
所以有。
1.4 对撞
当我们考虑对撞的时候,事情就变得有趣起来了。我们选取图1中的进行分析。其中是家中是否失窃,是报警是否响起,是热带风暴是否发生。像前面一样,我们也讨论是否被固定的情形。
不固定
在不固定时,或都很有可能导致。当观测到时,没有充足理由证明还是抑或是二者兼而有之。进一步地,在中间变量没有取值时,两侧的节点没有影响。也就是说,在不固定对撞结构的中间变量时,两侧变量之间的信息交流被阻断(如下图所示)。
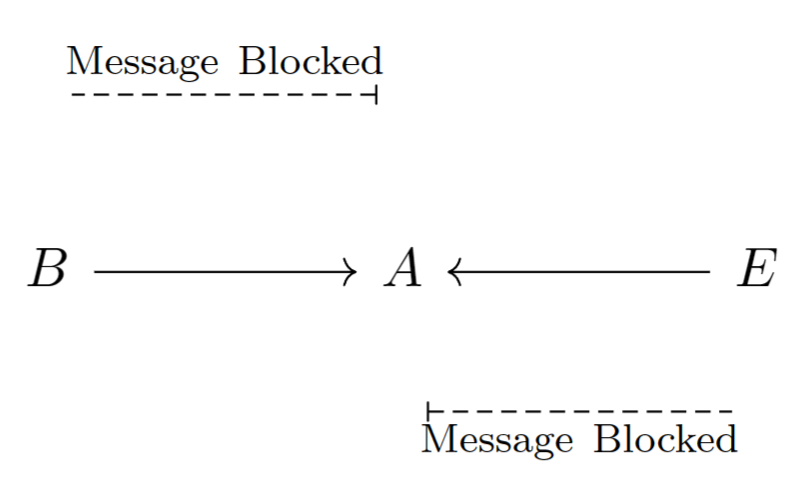
固定
在固定了中间变量时,神奇的事情发生了:如果固定时,如果和中有一个为,则另一个一定为;相应地,如果固定,则和大概率都为零。所以在固定对撞结构的中间变量时,两侧变量会相互影响,如下图所示。这件事情有一个直观的解释:假设成为名人至少需要才华和美貌中的一样。如果一个名人是一个具有精湛演技的演员,你就可以做出“辩解”,他/她不需要比普通人更漂亮了。这里也涉及一个对撞结构,而确定中间变量之后造成的两端变量相互影响的现象也被称为辩解效应。
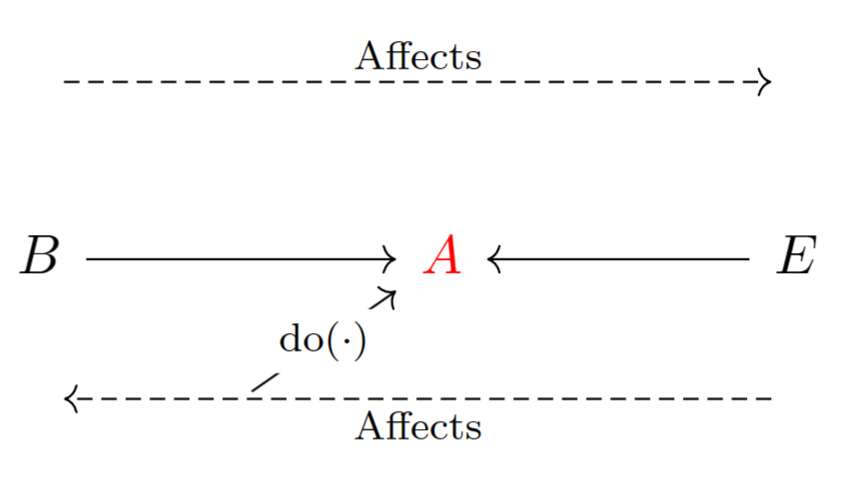
联合概率
最后我们通过概率透镜来看这样的现象。首先考虑联合概率
在不给定中间变量的取值时,有
这说明了当没有给定时,两变量是独立的,即,其中表示的取值未知。
当给定了的取值时,会得到一个丑陋的表达式:
蓝色的这一项不一定为,所以。
为了加深读者对对撞结构的印象,这里再提供一个自己的例子。
示例:硬币和闹钟
假设有一个闹钟,它是否闹铃取决于掷两枚硬币的结果。只有当两枚硬币不全是正面时,它才不会响。记两枚硬币的抛掷结果的随机变量分别为和,闹钟是否闹铃为,则可以绘制出下面的表格
| 正 | 正 | ||
| 正 | 反 | ||
| 反 | 正 | ||
| 反 | 反 |
在不观测结果之前,我们有(边缘独立),但一旦观察到或固定时,和不再相互独立。
接下来我们对原问题做一些修改:我们通过一个报告员来得知闹钟是否响起,且在闹钟没有响起时,有的概率误报。原来的表格进行修改后如下:
| 正 | 正 | |||
| 正 | 反 | |||
| 反 | 正 | |||
| 反 | 反 | |||
| 反 | 反 |
此时如果无视结果和闹钟结果(这其实也是自然地,因为在修改后的问题设定里面我们无法直接得知闹钟的状态)我们也可以发现和是独立的,而固定后和不再独立。如果把这个问题的因果图画出来,将会是下面这样:
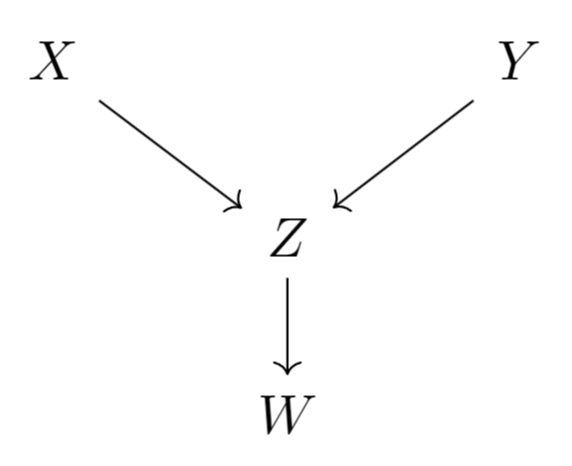
通过这个实例我们可以做出如下总结:
- 在未给定中间变量及其后代的取值时,对撞结构两侧变量互相独立;
- 在固定中间变量或中间变量的后代的取值时,对撞结构两侧的变量相互依赖;
- 没有因果关系的两个变量也可以有相关关系。
我们在借用Monty大厅问题(Monty Hall problem,也称羊车门问题)作为本节的结束。
示例:“羊车门”问题
在某个电视节目中,有三扇关闭的门。其中一扇门后面有汽车,其他两扇门后面各有一只山羊。参赛者首先选择一扇门,然后主持人会将一扇后面有山羊的门打开,然后询问参赛者是否更换自己的选择。我们设参赛者开始选择的门为,汽车的位置为,主持人打开的门为。我们可以这样考虑:假设参赛者选中了后面有车的门(概率为三分之一),则主持人可以打开剩下的门中的任何一扇;如果参赛者选中了后面有山羊的门(概率为三分之二),则主持人别无选择,因为剩下两扇门中一扇后面有汽车,根据规则主持人只能打开另一扇门。因此参赛者更换自己的选择获得轿车的概率更大。我们可以画出这个问题的因果图:
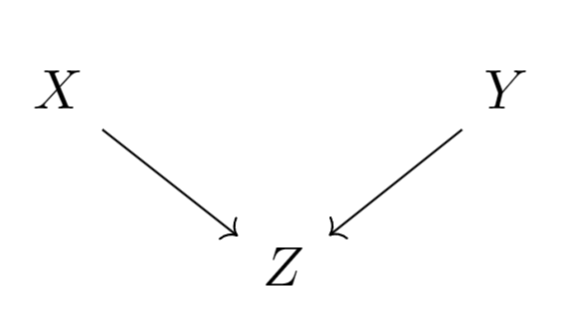
通过因果透镜重新审视问题,则答案昭然若揭:主持人一旦做出选择,相当于固定了的值。对撞结构使得和不再独立。
2 d-划分
实际的图模型往往会比较复杂,一对节点变量之间往往存在多条路径。在这种情形下,我们需要对图形中的节点变量的独立或依赖关系进行判定,也就是我们要讲解的d-划分。
2.1 d-划分的概念
d-划分(Directed Seperation,也称有向分割) 是一种在复杂图结构下依据节点变量之间的连接关系,分析节点变量之间相互独立或相互依赖关系的方法。简单而言,如果两个变量之间的每一条路径都被阻断,则这两个节点是d-划分;否则称两个节点是d-连接。上面涉及到三个重要的细节:
- 如果两个节点是d-划分,则二者之间的所有路径都需要被阻断
- 对于某一条路径,当其上的一点被阻断时,这条路径便被阻断
- “阻断”是指统计依赖关系的阻断。如果两个节点之间的唯一路径被阻断,则这两个节点对应的变量相互独立
对于一条连接两点的路径,如果满足下面的条件,则该路径被变量集合在取得特定值时阻断:
- 路径中存在对撞结构,对撞节点(中间点)及其后代节点也不在中
- 路径中存在链或分叉结构,且有至少一个节点在中
回忆上一节有关三个基本结构何时阻断的内容,不难推出。
现在给出d-划分的正式定义:
定义:d-划分
一条路径被节点集合阻断,也就是在集合中的元素都有取值时阻断,需要满足下面条件中至少一条
- 中包含链式结构或分叉结构时,,
- 中包含,。
进一步地,如果节点和之间的所有路径均被阻断,则和被集合所d-划分,即,这称为条件d-划分。如果,则这样的d-划分称为无条件d-划分。
使用d-划分可以让我们在不直接触碰严格的函数关系的情况下快速判断两个节点之间是否统计独立。这是使用图模型表达因果关系的优势。
示例
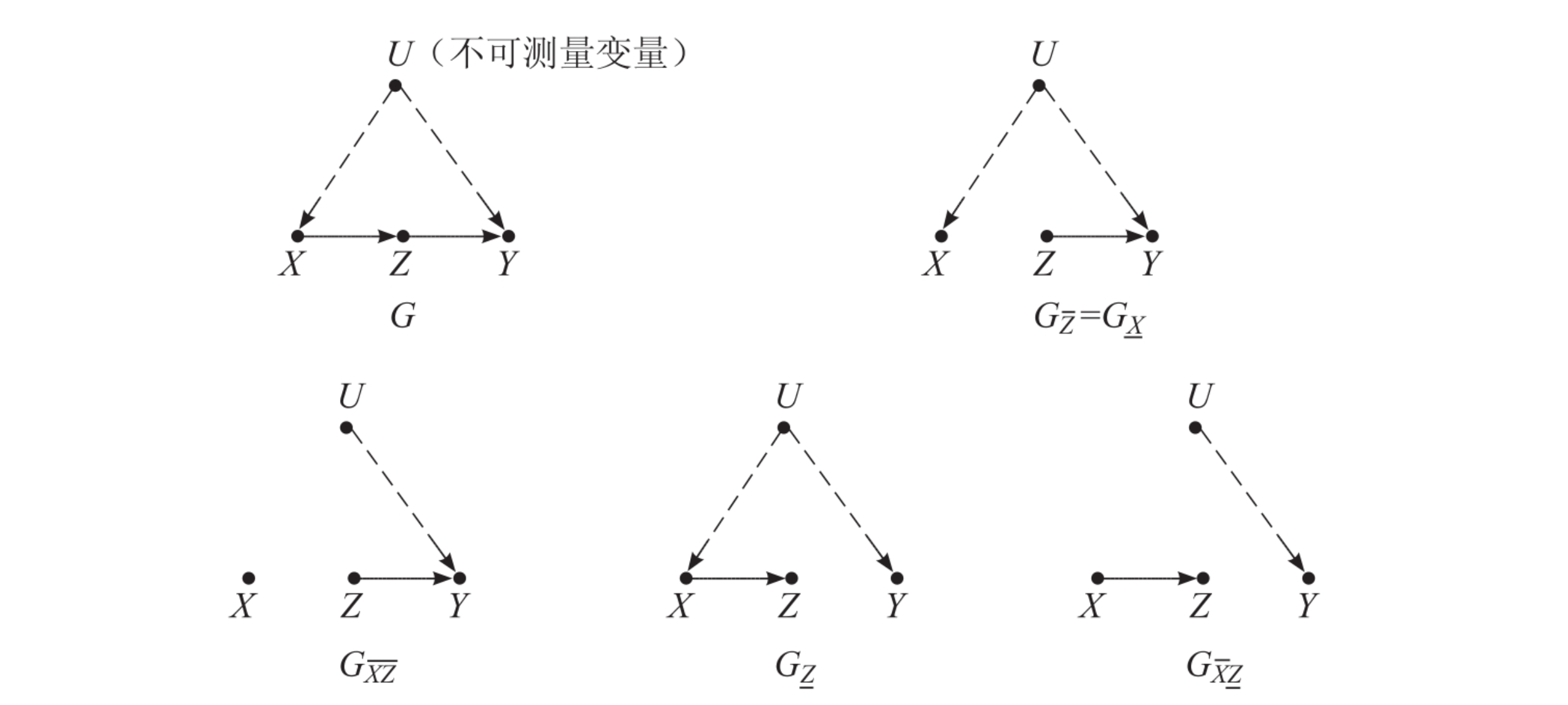
分析下面图模型中节点和之间的统计关系。
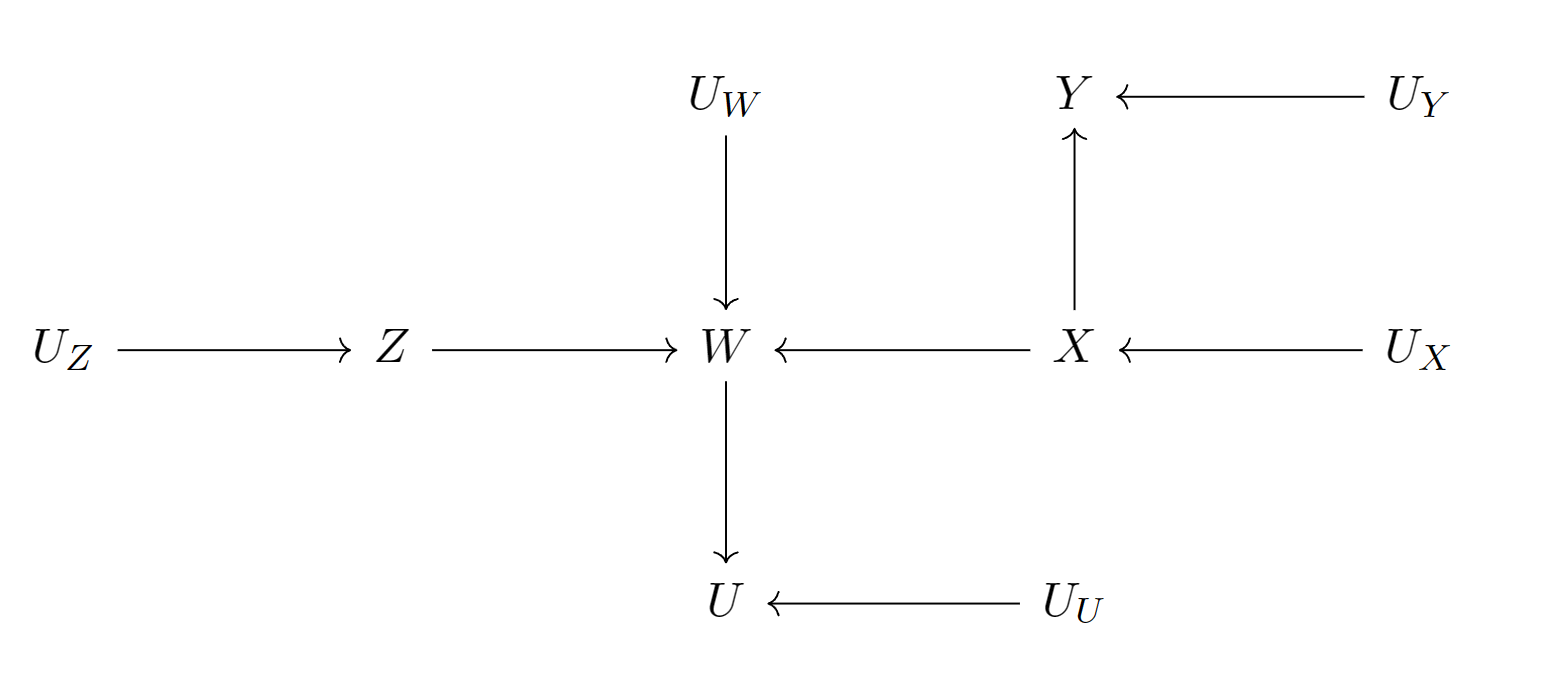
- 以节点为条件
- 对撞结构将被联通,节点和形成d-连接
- 以节点为条件
- 虽然对撞结构被打开,但随即因为固定了中间结点而被阻断。所以节点和形成d-划分
现在我们将图变得复杂一些:
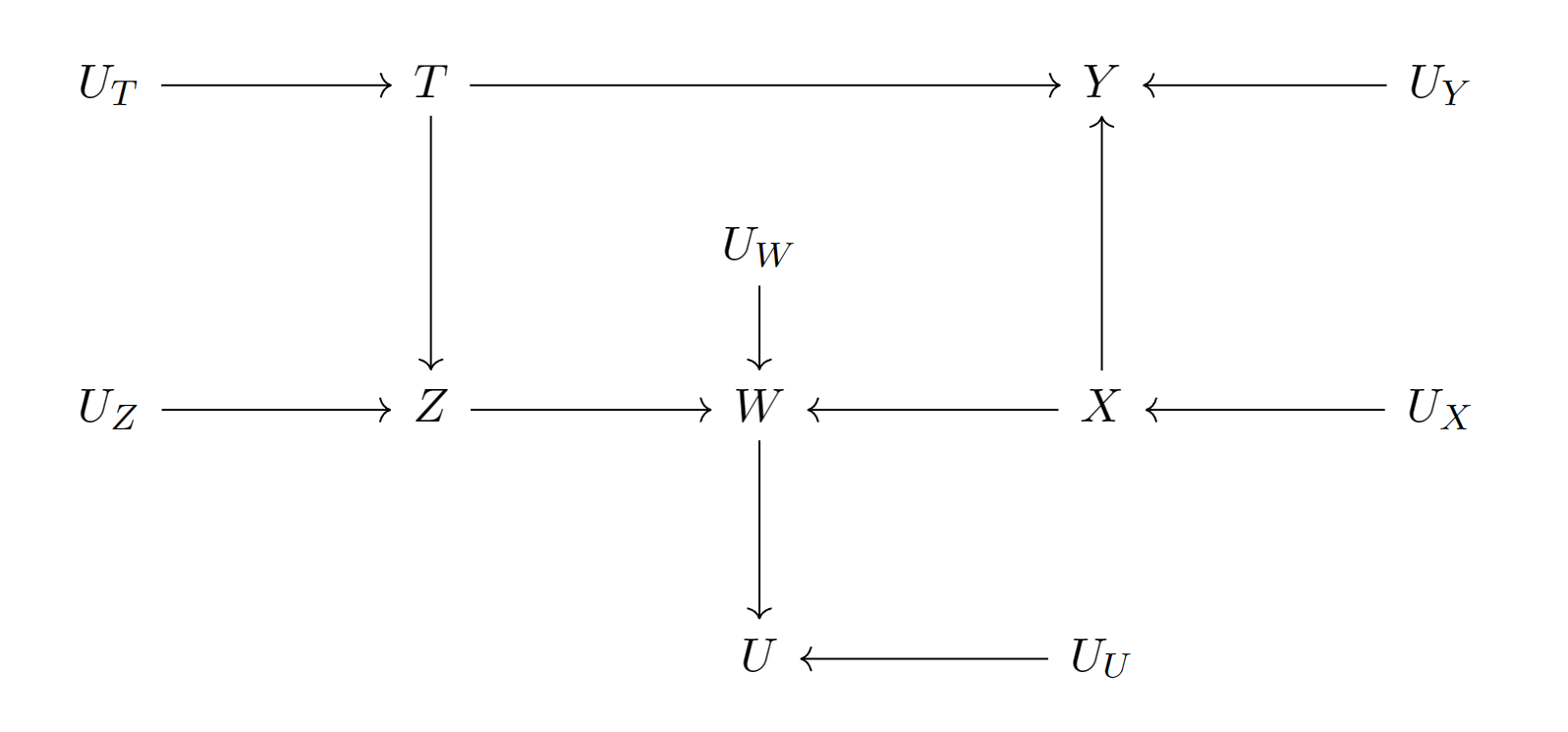
根据观察,我们可以得出下面的结论:
- 增加了一条路径,如果不固定,则节点和形成d-连接:
- 如果取集合为,则节点和形成d-连接,因为虽然阻断了,但打开了
- 以此类推
可以验证下面的图中蓝色的集合使得二者变为d-连接,红色的集合使得二者变为d-划分:
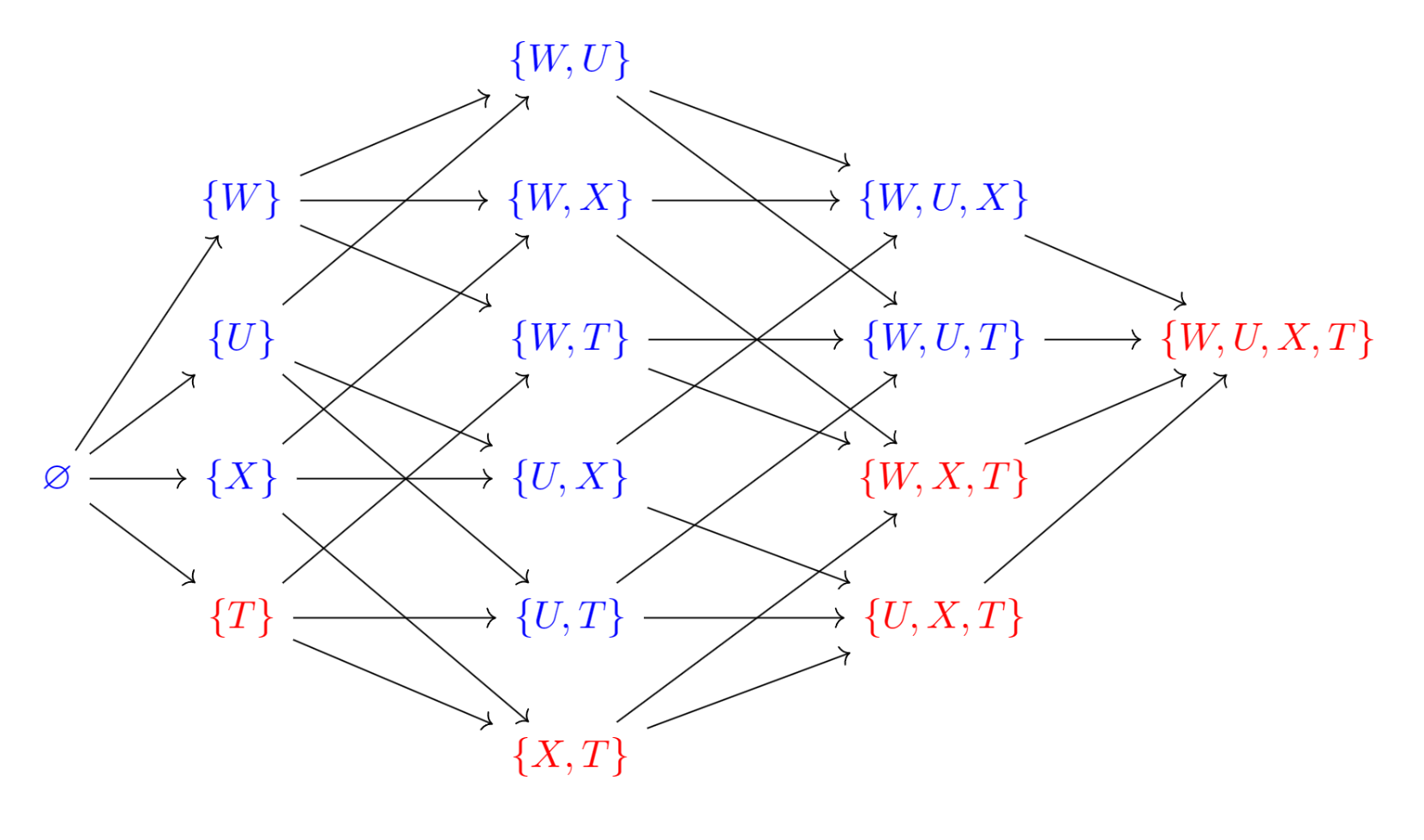
现在从Markov性的角度看。对于节点,如果所有外生变量相互独立,则给定其父母节点的条件下,节点与所有非后代节点都独立,即与和都独立。这是因为在给定的条件下,路径被截断,而中天然存在的对撞节点阻断了这条通路。
我们可以将上述推导过程推广值一般的有向无环图模型中。如果所有的外生变量相互独立,对于节点变量,给定其父母变量的条件下,节点和所有其非后代节点之间相互独立。进一步,假设是的一个子女节点,是的一个非后代节点,可见节点和之间不可能通过各自的外生变量建立d-连接。所以分析二者之间的关系秩序分析经过内生变量的路径。这些路径分为通过其父母节点的路径(后门路径),和通过其子女节点的路径(前门路径)
考虑后门路径,由于箭头从,所以控制可以阻断这条路径
由于不是的后代节点,则从到的路径中一定有一处箭头反向(从方向指向)不妨假设它是(如下图),则一定存在一处对撞结构,这样的路径也被阻断。
图13:关于统计独立性的更一般讨论 因此对于有向无环图,节点变量和非后代变量之间在所有外生变量之间相互独立,且给定节点变量的父节点的条件下,无论从前门还是后门都无法建立d-连接。因此在此条件下与所有非后代节点之间相互独立。
2.2 d-划分的判断
如果按照上面提出的判断方法,我们需要判断两个节点之间的所有路径是否被阻断,这显然十分麻烦。我们一般将图转换为无向图,然后在无向图中判断节点或节点集。在介绍具体方法之前,先引入一些定义。
定义:祖先图(Ancestral Graph)
祖先图地原图的一个子图,进包括判断条件独立性概率表达式中提到的变量及其祖先
定义:道德图(Moral Graph)
图是一个有向无环图,对于图中任意节点,若二元组,则在图中添加一条无向边,并将图中素有无相边改为有向边,得到图的道德图
定义:无向划分
给定图,,和是图中三个互不相交的节点集,分别是中的节点。如果连接和的任何一条路径中都含有中的节点,则称在无向图中分隔了和,简称为“和被无向划分”。
下面不加证明地引入一个和无向划分和d-划分有关的定理:
定理(Lauritzen)
设是一个有向无环图,,和是图中三个互不相交的节点集。是包含中三个节点集及其各自祖先节点的祖先图,是的道德图,则和在中为所d-划分当且仅当和在中被无向划分。
根据上面的定理,我们可以构建出一个判断d-划分的流程:
- 画祖先图 — 根据条件独立性概率表达式涉及的节点构建祖先图
- 画道德图 — 将祖先图中拥有相同的子女节点的节点之间使用无向边相连(若一个节点有多个父母节点,则将其两两相连)最后将整个图无向化
- 删除条件 — 对于解决的问题,删除其中涉及的条件变量(在给定xxx条件下的“xxx”)得到结果图
- 判别 — 应用 Lauritzen 定理判断目标节点是否有边直接相连,如果没有直接相连的边,则说明目标变量给定条件下相互独立。
示例
考虑下面的图模型,判断下面的问题
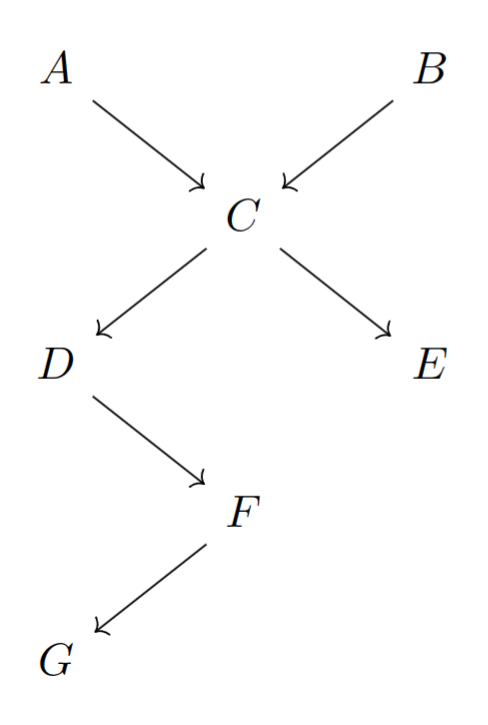
- 请问和是否在给定和的条件下相互独立?
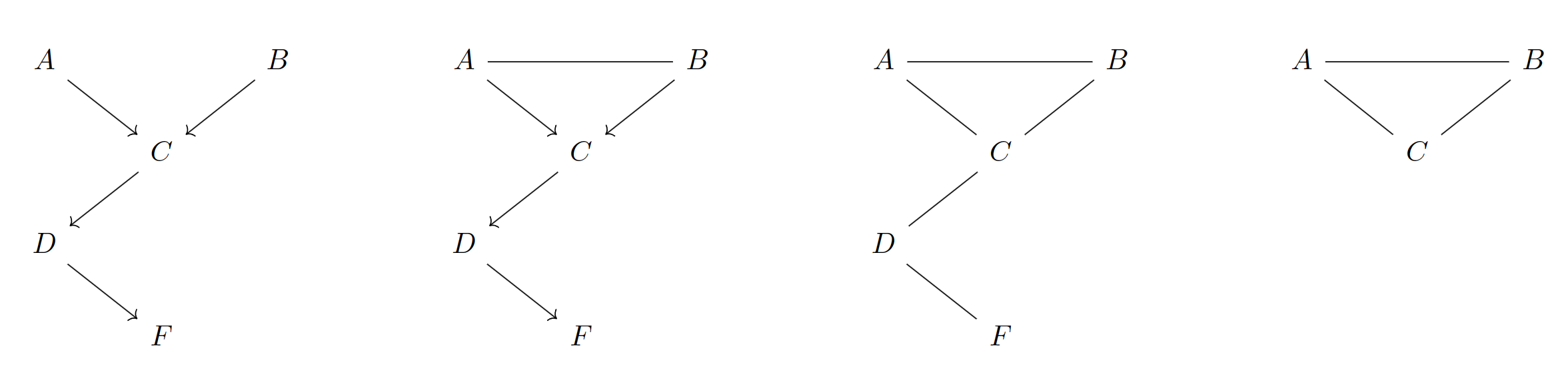
由图可知,和在给定条件下相互不独立。
- 请问和是否边缘独立?

由图可知,和边缘不独立。
- ,
本问题相当于:在给定时,是否既和独立,也和独立?
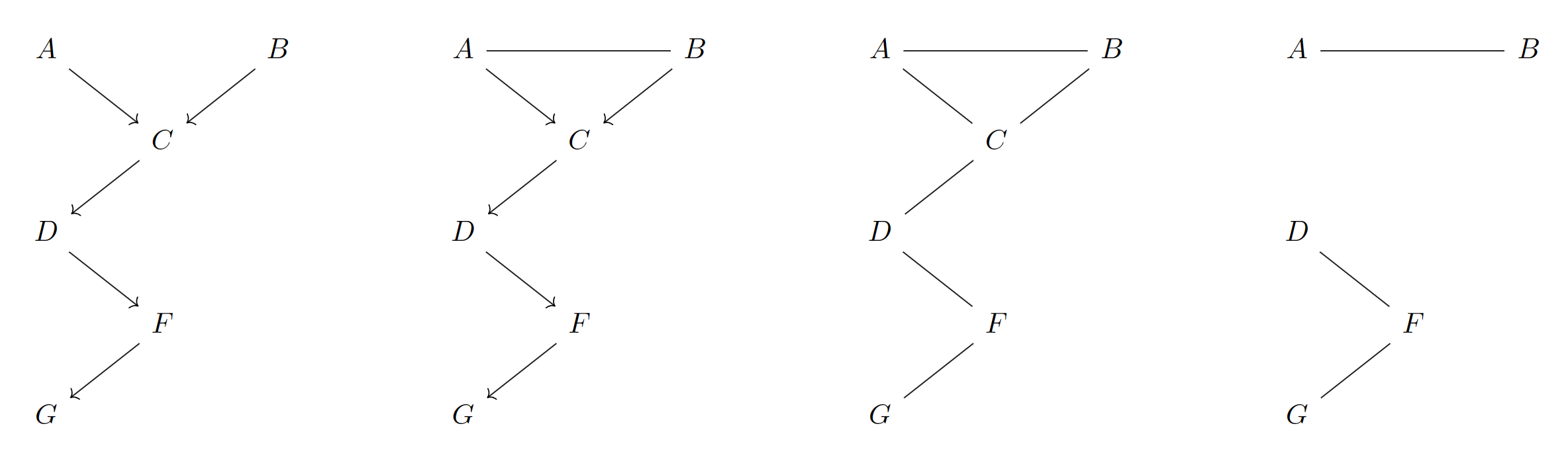
由图可知,与相连,于是两个要求中有一个无法满足。因此。
2.3 d-划分变量集合搜索
在上一节中,我们主要解决的问题是形如“给定xxx条件,问xxx和xxx是否相互独立”这样的问题。本节我们探讨形如下面的问题:给定有向无环图,已知其中的两个不交集合和,找一个节点集合,使得和被所d-划分,即
首先引入有效链的概念:
定义:有效链(Active Chain)
对于图模型中任意路径上任意无向连续相连的三个节点,如果,且满足下面两个条件之一,则称这三个节点针对节点变量集合构成一个有效链(说的其实是信息可以通过这个结构):
满足不是对撞结构,且
满足是对撞结构,且
在给定节点变量集合的情况下,有效链两端的节点变量相互联通,请看下面的例子:
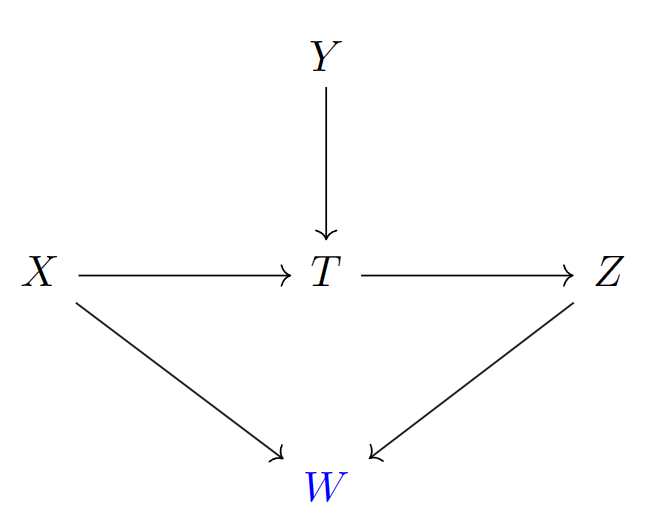
在图18中,假设节点集合为,则、、、和为有效链,而不是有效链。
我们回到本节开始时提出的那个问题:如何在给定有向无环图中不交节点集和的条件下,找到一个节点集使得它和被所d-划分。针对中的每个节点,找到在给定下与其d-连接的所有节点集合,则。这样一来,原问题被简化为下面的形式:对中的一个节点,如何找到给定情况下与其d-连接的所有节点变量的集合。为了做到这一点,可以找中所有和相连的边,如,并将该边标记为,再根据找到,判定给定的条件下是否构成有效链。如果构成有效链,则将边标记为,并将和放入集合中,同时将替换为,替换为,递归地进行上面的步骤,直到找不到有效链为止。最终得到。
在算法的实际实现中,我们从开始,逐步向外扩展我们找到的有效链。而算法中往往在上叠加反向箭头得到。这样做是有道理的:在图18中,假设,,现在寻找合适的。链中的被和中的边标注为,从而漏掉了。如果添加反向边,则可以引导算法找到这条被漏掉的路径,如下图所示(我们没有修改原图的结构)。