【基于图模型的因果推断】3 图模型和结构因果模型：理论和简单实践

7 因果关系的表示：图模型与结构因果模型

7.1 因果关系的概念

这里考虑马哲对因果的定义：因果关系为时间之间的特定关系，在此关系下，一些时间的发生将导致另外一些事件的发生，相应称前者为后者的“原因”，后者为前者的“结果”

考虑时间$A$有多个因的情况，分下面两种情况：

• （必要因）作为因的多个事件单独都不足以导致$A$的发生，必须所有事件都发生才能导致$A$的发生
• （充分因）作为因的多个事件只要有一个发生，就能导致$A$的发生

事件之间的因果关系拥有如下性质：

• （传递性）若$A$是$B$的因，$B$是$C$的因，则$A$也是$C$的因
• （非反身性）一个事件不是它自己的因
• （非对称性）若$A$是$B$的因，则$B$一定不是$A$的因

可以发现，这里的定义其实和 严格偏序 是对应的。而严格偏序和有向无环图有一一对应关系。所以我们下一小节将会讲到图

假设事件集合$\mathcal{A}$中的事件都是事件$B$的因，当$\mathcal{A}$中的事件发生后，事件$B$的发生与否和事件$B$的其他因无关（即事件集合$\mathcal{A}$中的事件的发生把$B$的其他因的效果屏蔽了），则称$\mathcal{A}$中的事件为$B$的直接因 (Direct Cause)，$B$的其他因则为它的间接因 (Indirect Cause)。

对于这种情况，可以做这样的考虑：火灾报警器一定程度上指示火灾是否发生，但如果一个房间从外观上看起来已经失火，那么其中的火灾报警器是否报警在确认房间是否失火这件事上已经对我们没有任何帮助了。

一个事件对另一个事件是直接因还是间接因取决于特定的分析场景。若不考虑其他事件，则划火柴($C$)是火柴被点燃($A$)的直接因；但如果考虑温度、氧气等火柴燃烧的条件($B$)时，$C$就不再是$A$的直接因。事实上，$B$是$A$和$C$的因果中介。

我们可以使用数学语言将上面的内容形式化：假设事件集合$\mathcal{V}$是包含事件$X$和$Y$的集合，取$\mathcal{C} \in 2^{\mathcal{V} - \{ Y \}}$。若满足下面的条件，则在给定$\mathcal{V}$的条件下，$\mathcal{C}$中的元素（事件）$X$是$Y$的充分因：

1. $\mathcal{C}$中的所有事件都是$Y$的因
2. 若有$\mathcal{C}$中的事件发生，则事件$Y$的发生与集合$\mathcal{V} - (\{ Y \} \cup \mathcal{C} )$中的任何事件是否发生无关
3. 集合$\mathcal{C}$中没有其他真子集满足 (1) 或 (2)

类似地，可以定义变量之间的因果关系。在变量系统$\mathcal{S}$中，若存在事件$E$，其中的变量$\mathrm{q}=q$时会导致变量$\mathrm{r} = r$，则称$Q$是$R$的因。进一步地，我们也可以定义变量的直接因。为了和上面做区分，我们适当变换相应的记号：变量集合$V$是包含变量$\mathrm{x}$和$\mathrm{y}$的集合，取集合$C \in 2^{V - \{ \mathrm{y} \}}$。若满足下面的条件，$C$中的变量$\mathrm{x}$是变量$\mathrm{y}$的直接因：

1. $C$中的变量都是变量$\mathrm{y}$的因
2. $C$中的一个变量$\mathrm{x}$取到了特定取值集合$\mathbb{x}$中的某一个值时，变量$\mathrm{y}$将取值$y$；且此时该变量的取值与集合$V - (\{ \mathrm{y} \} \cup C)$中的任何变量的取值无关
3. $C$没有其他真子集满足 (1) 和 (2)

$2^{X}$表示$X$的幂集，表示$X$的所有集合构成的集合。对于有限集，有$\left|2^{X}\right| = 2^{|X|}$。

7.2 图模型

图是一组资料$\mathscr{G} = (\mathcal{V}, \mathcal{E})$，其中$E$是$V \times V$的一个子集。$V$被称为节点 (Vertex) 集合，$\mathcal{E}$被称为边 (Edge) 的集合。如果$(v_{1}, v_{2}) \in E$，则在直观上有一条从$v_{1}$指向$v_{2}$的有向边 (Directed)。如果$v_{1}$和$v_{2}$的边是无向的 (Undirected)，则$\{ (v_{1}, v_{2}), (v_{2}, v_{1}) \} \subset E$。进一步地，如果一个图是无向的，它的邻接矩阵 (Adjacency Matrix)$A$是对称的。对于有向图，有“入”和“出“的概念。举上面的边$e = (v_{1}, v_{2})$为例，$v_{1}$是一个射出节点，$v_{2}$是一个射入节点。

对于节点数有限的图$\mathscr{G}$，其邻接矩阵$A \in \text{Bool}^{|G| \times |G|}$是方阵，其中$A_{i,j}$的值表示图中的是否存在一条从节点$v_{i}$指向$v_{j}$之间有向边。

在因果推断的讨论中，我们通常取一个路径 (Path)，即$\mathscr{G}$所对应的无向图（其邻接矩阵为$A \vee A^{\top}$）的路径再自然投射到$\mathscr{G}$​​上的结果。下面是一个简单的例子：

图1：一个路径的简单例子。可以理解为先在无向图中选定一个路径，然后投射向有向图

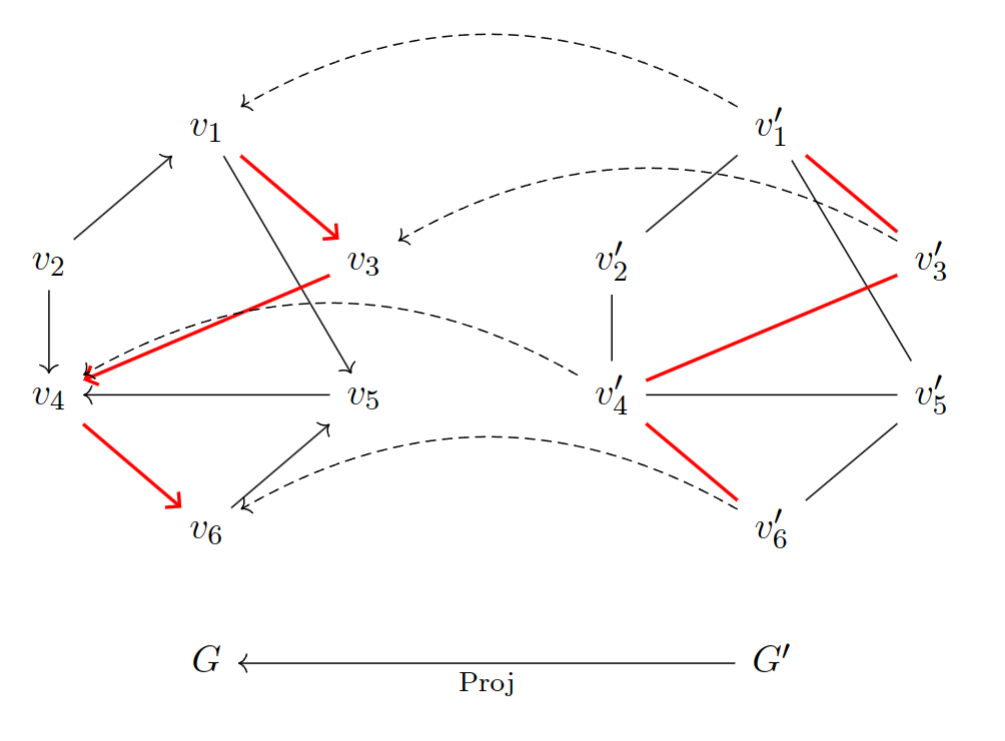
这里的一个路径（红色）可以写为$v_{1} \rightarrow v_{3} \rightarrow v_{4} \rightarrow v_{6}$

箭头不一定要朝着一个方向，因为我们在以后的讨论中需要涉及到类似对撞这样的结构：

$$A \rightarrow {\color{red} B} \leftarrow C$$

在这个对撞结构中，$B$被称为对撞因子。上面的例子没涉及到这样的情况纯粹是因为我画图的时候恰好选了一条箭头方向都一样的路径，而且我不想重新画过了（瘫）

最后我们引入环的概念。在有向图中，可以沿着箭头在图上行走。如果沿着箭头行走回到了原点，则走过的路径是一个环。例如图1中的$(v_{4}, v_{6}) \rightarrow (v_{6}, v_{5}) \rightarrow (v_{5}, v_{4})$。在我们的设定中，无向图是有向图的一个特殊形式，显然只要在无向图中发现类似地结构，也是一个环。例如在图1中右侧的无向图中除了$\{ v_{4}', v_{5}', v_{6}' \}$成一个环，$\{ v_{1}', v_{2}', v_{3}', v_{4}' \}$也成一个环。

---

7.3 结构因果模型 (Structural Casual Model, SCL)

结构因果模型是这样一组资料：$(U, V, \mathcal{F})$，其中$U$为外生变量集合，$V$为内生变量集合，$\mathcal{F}$为量化关系的函数集合。

例子：分析影响考试成绩的因素
考试时老生常谈的问题。人们一般认为，考试成绩($\mathrm{y}$)的因有学生智商($\mathrm{i}$)、课余学习时间($\mathrm{t}$)、家庭对教育的重视程度($\mathrm{f}$)和教师水平($\mathrm{l}$)。我们可以构建上述变量之间的因果模型：

$$\begin{align*} \mathrm{i} &:= \mathrm{u}_{1}, \\ \mathrm{f} &:= \mathrm{u}_{2}, \\ \mathrm{t} &:= \mathrm{f} + \mathrm{u}_{3}, \\ \mathrm{l} &:= \mathrm{u}_{4}, \\ \mathrm{y} &:= f^{\mathrm{y}}(\mathrm{i}, \mathrm{f}, \mathrm{t}, \mathrm{l}, \mathrm{u}_{5}). \end{align*}$$

其中$\mathrm{u}_{5}$是除了上述这四个内生变量之外的所有因素。另外，我们注意到内生变量$\mathrm{t}$，即课余学习时间也受到一些不确定因素$\mathrm{u}_{3}$的影响。我们可以构建这个问题中的内生变量集合$V = \{ \mathrm{i, f, t, l, y} \}$，和外生变量集合$U = \{ \mathrm{u}_{1}, \mathrm{u}_{2}, \mathrm{u}_{3}, \mathrm{u}_{4}, \mathrm{u}_{5} \}$。外生变量的取值不受内生变量的影响。其不同的取值集合代表不同的场景（例如不同收入、文化水平的家庭等等）。需要注意的另一个细节是方向性。例如第一个式子$\mathrm{i} := \mathrm{u}_{1}$，表示变量$\mathrm{i}$听命于变量$\mathrm{u}_{1}$，数值上彼此恰好相等，但其作用是单向的（请允许我稍滥用一下符号）。单向说的是改变$\mathrm{u}_{1}$会导致$\mathrm{i}$的改变，反之则不然（鸡不叫，太阳照公常升起）。

7.4 图模型和结构因果模型的比较

• 每个结构因果模型对应一个图模型
• 一个图模型可能对应多个结构因果模型，因为当结构因果模型转换为图模型时，内生变量和外生变量融合为节点集合$V$，而其他的假设被遗忘了

上面的例子对应下面的图模型：

图2：学生成绩问题对应的图模型，其中红色为外生变量，蓝色为内生变量（尽管如此，它们在图模型中都是对等的节点）

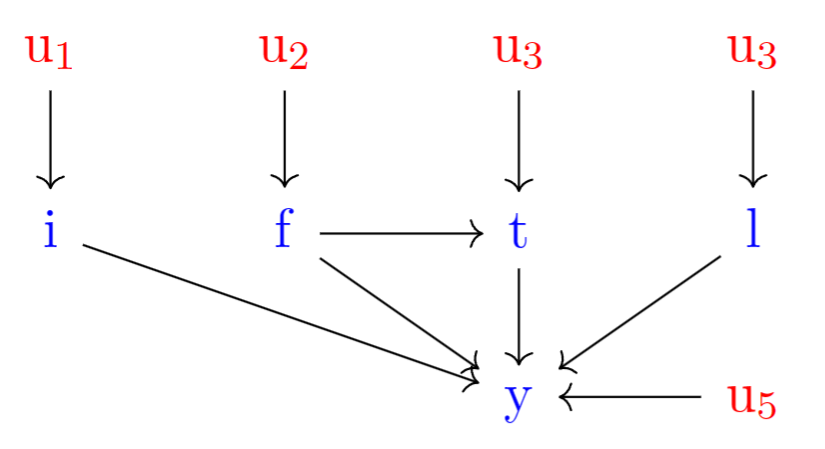
从这个图模型中可以看出，它无法精确提供变量之间的准确函数关系，即变量之间具体是如何互相影响的。在实际工作中，我们常常使用图模型获取变量之间的定性关系即可，而这是简洁直观的图模型易于做到的。另外，大多数应用场景中，我们往往省去外生变量。

8 因子分解

在因果推断中，我们常常见到多个变量的联合概率分布（在学生成绩的例子中，如果变量都取自一个概率分布，则学生成绩这个变量取自它的因的某个联合分布）。联合分布有下面两种表达方式：

1. 表格（每一个表示一个组合的概率，直观易懂，但当变量数越来越多时就会显得臃肿）
2. 函数（使用多个函数表达变量之间的关系，并结合外生变量的概率分布）
   • 如果不知道具体的函数关系，则写不出具体的表达式
   • 外生变量的分布难以量化
   • 及时得到的多个变量的函数表达式，求解联合分布十分困难

如果我们在此引入图模型，多个变量的联合分布将得到简化。进一步，当图模型具有Markov性时，联合分布可以根据链式法则进行分解，这称为因子分解。

8.1 图模型的 Markov 性

为了叙述的方便，我们先引入图模型的Markov性的定义：

定义（有向无环图模型的 Markov 性）
有向无环图$\mathscr{G} = (\mathcal{V}, \mathcal{E})$中，$W$是$V$的任意子集，记$\text{Parents}(W)$为节点集合$W$的所有父母节点组成的集合，$\text{Descendents}(W)$为集合$W$所有后代节点组成的集合。在给定$\text{Parents}(W)$的条件下，节点变量集合$W$独立于$\mathscr{G}$中$W$的所有非后代节点（不含父母节点），则称$\mathscr{G}$具有Markov性。

为了理解上述的定义，考虑下面两个例子：

图3：两个Markov图模型的例子

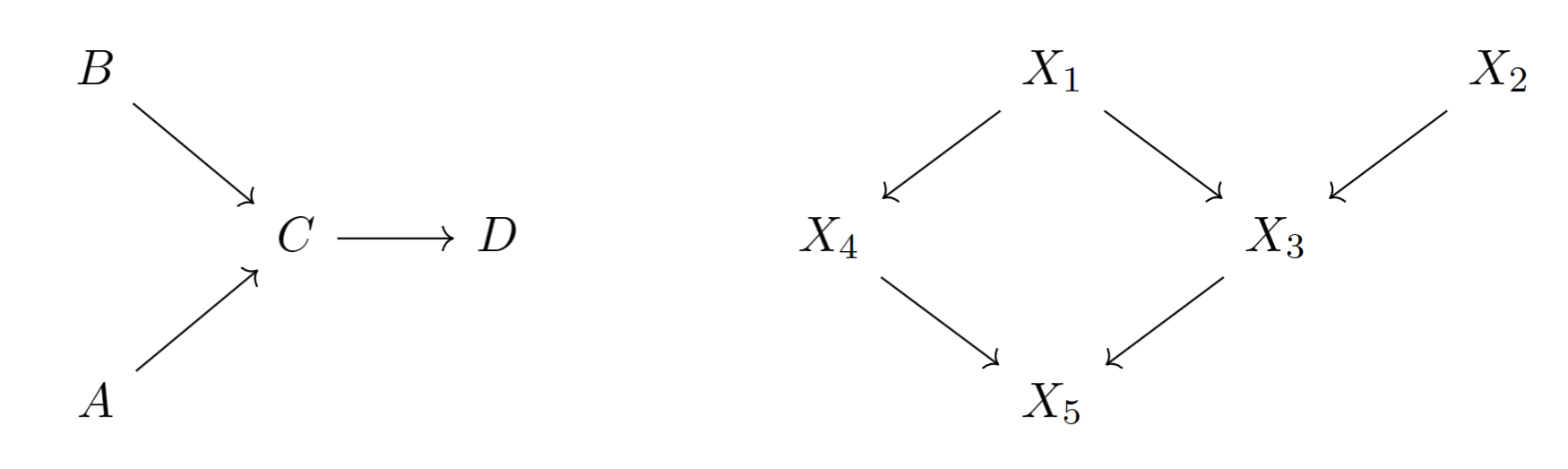
在考虑的时候，请牢记：相互独立的是不含父母节点的非后代节点</big>，然后不难发现下面的几组节点相互独立（抱歉，这里虽然看起来没有滥用符号，但其实是滥用符号。因为我只是把两个垂直符号叠在了一起，书上那个奇奇怪怪的玩意儿在markdown里面不能直接打出来）：

• $A \perp\!\!\!\perp B$,
• $D \perp\!\!\!\perp \{ A, B \} | C$（给定$C$的条件下独立）,
• $X_{1} \perp\!\!\!\perp X_{2}$,
• $X_{2} \perp\!\!\!\perp \{ X_{1}, X_{4} \}$,
• $X_{5} \perp\!\!\!\perp \{ X_{1}, X_{2} \} | \{ X_{3}, X_{4} \}$,
• $\{ X_{4}, X_{5} \} \perp\!\!\!\perp X_{2} | \{ X_{1}, X_{3} \}$,
• … （剩下的请你自己找出来）

8.2 因子分解表达式

定理：因子分解
对于有向无环图的模型，记其节点变量的集合为$\{ x_{1}, \dots, x_{n}\}$，则其联合概率

$$P(x_{1}, \dots, x_{n}) = \prod\limits_{i=1}^{n} P\Big(x_{i} \Big| \text{Parents}(\{ x_{i} \})\Big)$$

证明：根据链式法则，有

$$P(x_{1}, \dots, x_{n}) = \prod\limits_{i=1}^{n} P\Big(x_{i} \Big| x_{1}, \dots, x_{i-1}\Big)$$

其中规定$P(x_{1}|x_{1}, \dots, x_{0}) = P(x_{1})$。由于图模型的Markov的，因此对于任意$x_{i}$，有

$$P\Big(x_{i} \Big| x_{1}, \dots, x_{i-1}\Big) = P\Big(x_{i} \Big| \text{Parents}(\{ x_{i} \}) \Big).$$

$\square$.

因子分解可以帮助剔除计算联合概率过程中不相关的部分，可以节省储存空间和计算成本。

9 图模型结构的程序实现

9.1 安装 R

参见R语言官网

• 清华镜像

安装完成后的启动界面：

图4：RGUI安装成功的启动画面

9.2 DAGitty包的安装与加载

在命令行中输入：

install.packages('dagitty')

随后根据信息指示点下一步即可

9.3 图模型的生成

下面给出一个简单的图模型建立的例子：

> library('dagitty')
> g <- dagitty('dag{
+                   X[pos= "0,1"]
+                   Y[pos= "1,1", exposure]
+                   Z[pos= "2,1", outcome]
+                   W[pos= "1,0"]
+                   T[pos= "2,2"]
+                   X -> Y -> Z -> T
+                   X -> W -> Y -> T
+                   W -> Z
+ }')
> plot(g)

下面是绘图的结果：

图5：使用dagitty构建的因果图模型

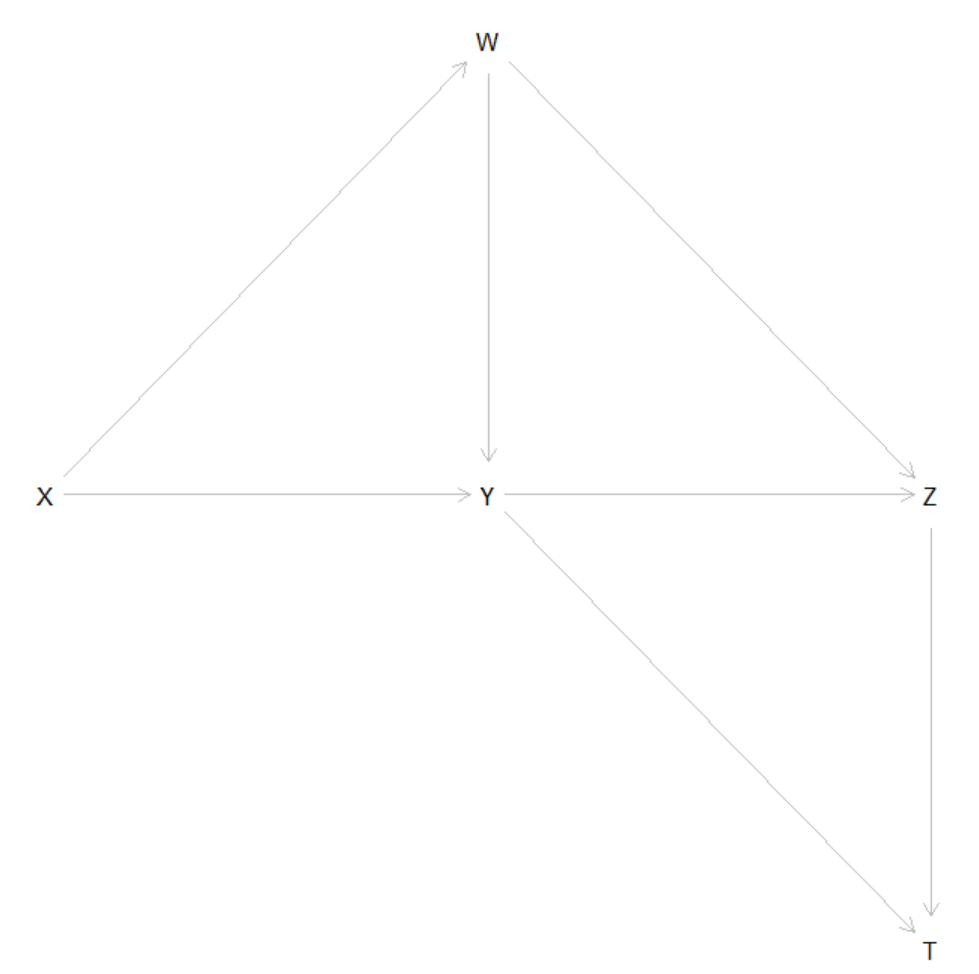
下面对代码做简要的解释

• +号表示多行输入，当需要多行输入时，换行时需按下<SHIFT><ENTER>
• dagitty(ˈdag{...}ˈ)表示生成有向无环图模型
• 箭头号<-（某些时候会被渲染成一个完整的箭头）将右侧的对象赋值给左边
• dag{...}中给出了图模型的具体定义
• Y[pos= "1,1", exposure]语句中
  • Y是节点名，如果节点名称中有空格等其他符号，需要使用双引号""
  • pos="1,1"表示其位置为$(1, 1)$
  • exposure或e表示该变量是干预变量，outcome或o表示该变量是结果变量，adjusted或a表示该变量是调整变量
• W -> Z表示图中有W指向Z的箭头，双箭头的表示方法是<->
• 为了便于阅读，各语句之间使用分号;隔开
• 关于箭头的简写
  • W -> Z -> C相当于W -> Z、Z -> C两条语句
  • X -> { W -> Z <- Y}表示从X出发，各有一条指向W，Z和Y节点的有向边

接下来介绍一些基本的计算

R代码	解释
parents(g, "E")	求解图g中节点"E"的父母节点
ancestors(g, "E")	求解图g中节点"E"的祖先节点
children(g, "E")	求解图g中节点"E"的子女节点
descendants(g, "E")	求解图g中节点"E"的后代节点
paths(g, "X", "T")	求解图g中所有从节点"X"到"T"的无向路径
paths(g, "X", "T", directed=TRUE)	求解图g中所有从节点"X"到"T"的有向路径

9.4 Python 的环境配置

对于使用Python的用户，这里简要讲解Python包DoWhy（DoWhy官方文档）

9.4.1 安装方法

打开终端，切换到合适的虚拟环境，然后输入

pip install dowhy

或输入

conda install -c conda-forge dowhy

9.4.2 简单图模型构建

构建简单的图模型时，需要用到包networkx，其安装方法和上面类似。下面给出一个简单的例子：$X \rightarrow Y \rightarrow Z$

import networkx as nx
from dowhy import gcm

causal_graph = nx.DiGraph([('X', 'Y'), ('Y', 'Z')])
causal_model = gcm.StructuralCausalModel(causal_graph)

在构建因果模型后，就可以使用库函数和数据进行推断了。由于后面的内容超出了目前的进度范围，请感兴趣的读者自行探索。