【DatawhaleML】 4 支持向量机

支持向量机 (Support Vector Machine)

1 间隔和支持向量

考虑二分类问题，其训练集为 $D = \{(\boldsymbol x_i, y_i)\}_{i=1}^m$ ， $y_i\in\{1, -1\}$ ，分类的主要目标为找到一个超平面，使得这个超平面可以将这两类样本尽可能分开，如下图所示。但对于有限的样本，可以将训练集正确分开的这样的超平面不止一个，我们需要选择一个“最好”的超平面作为我们的判别依据。

图1 二分类问题可能有多个超平面将训练集完全分开（来源：Wikipedia）

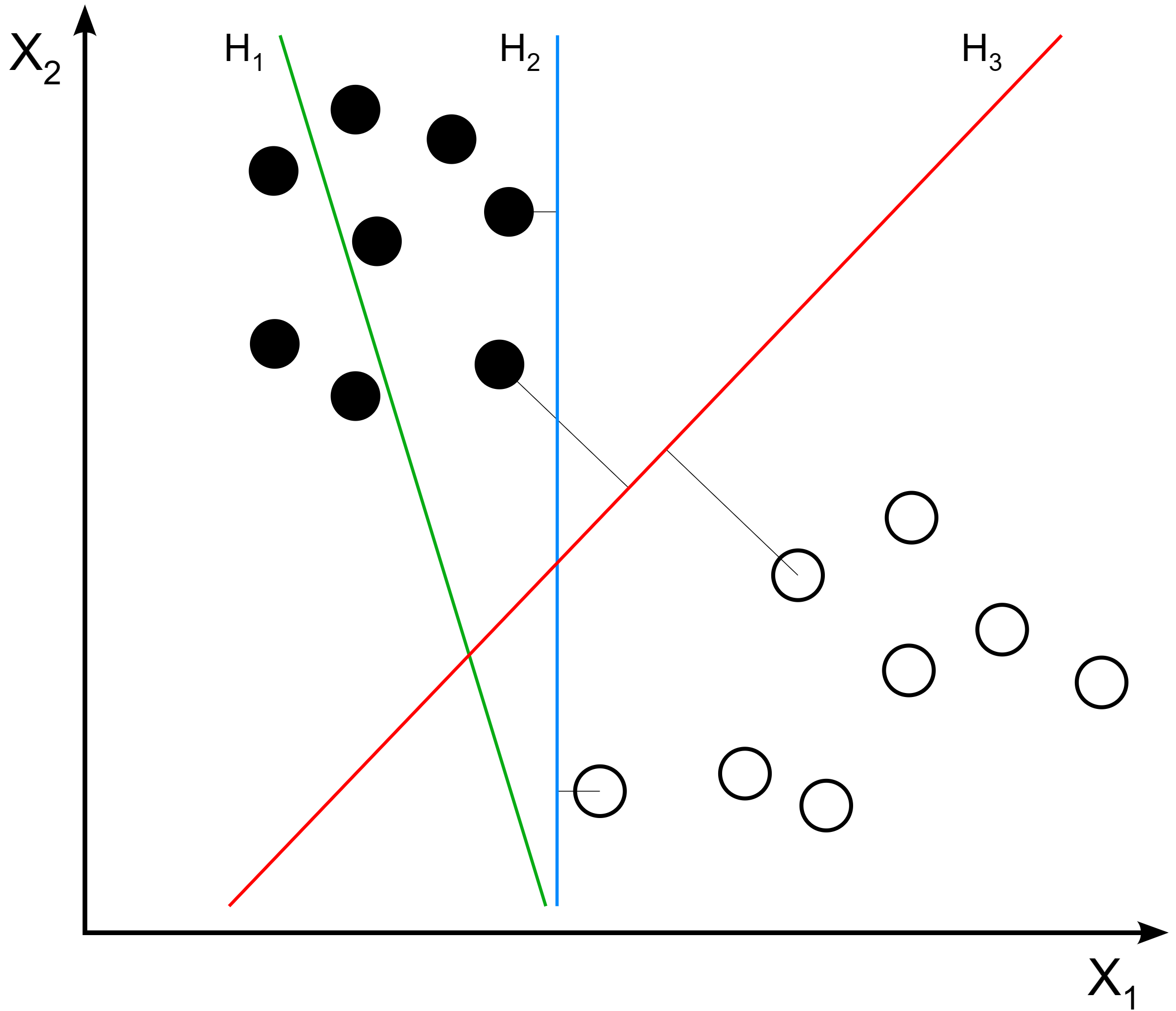
事实上，我们可以这样考虑。由于训练样本只是真实样本空间中的一个采样，在不断接受新样本的时候，我们希望在训练样本上训练得到的划分准则依然可以起到较好的作用，也即具有较好的鲁棒性 (Robustness)。具有这样特征的模型，我们也称它具有一定的泛化 (Generalisation) 能力。

超平面可由方程 $\boldsymbol w^\top\boldsymbol x + b = 0$ 确定，其中 $\boldsymbol w$ 为权重向量， $b$ 为偏置。样本空间 $\mathcal{X}$ 中的点 $\boldsymbol x$ 到超平面的距离为 $\displaystyle r = \frac{|\boldsymbol w^\top\boldsymbol x + b|}{\|\boldsymbol w\|}$ 。

点到超平面距离的计算

Reference

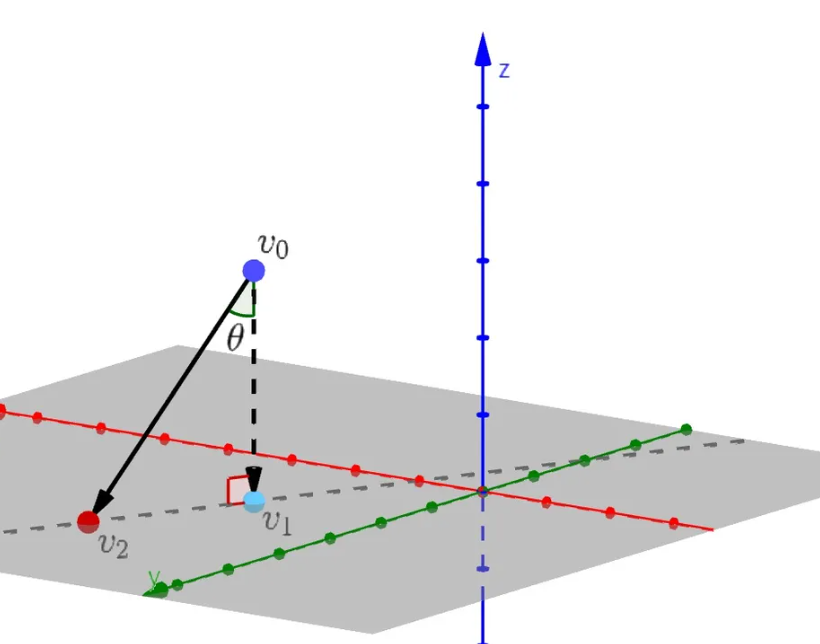
给定超平面外一点 $\boldsymbol x_0$ ，令 $\boldsymbol x_1$ 为 $\boldsymbol x_0$ 在超平面上的投影点， $\boldsymbol x_2$ 为超平面上任意一点，问题在 $\mathbb{R}^3$ 中的情形如下图所示。

于是 $r = \Big\|\overrightarrow{\boldsymbol x_0\boldsymbol x_1}\Big\| = \Big\|\overrightarrow{\boldsymbol x_0\boldsymbol x_2}\Big\||\cos \theta|$ 。根据向量夹角公式，有 $\displaystyle \cos\theta = \frac{\overrightarrow{\boldsymbol x_0\boldsymbol x_1}\cdot \overrightarrow{\boldsymbol x_0\boldsymbol x_2}}{\Big\|\overrightarrow{\boldsymbol x_0\boldsymbol x_1}\Big\|\Big\|\overrightarrow{\boldsymbol x_0\boldsymbol x_2}\Big\|}$ 。由于 $\boldsymbol w$ 是超平面的法向量，于是有 $\boldsymbol w\cdot \overrightarrow{\boldsymbol x_1\boldsymbol x_2} = 0$ 。又因为 $\overrightarrow{\boldsymbol x_0\boldsymbol x_1}$ 和 $\overrightarrow{\boldsymbol x_1\boldsymbol x_2}$ 垂直，于是存在某个 $k\in \mathbb{R}$ ，有 $\overrightarrow{\boldsymbol x_0\boldsymbol x_1} = k\boldsymbol w$ 。所以
$r = \frac {\Big|\overrightarrow{\boldsymbol x_0\boldsymbol x_1}\cdot\overrightarrow{\boldsymbol x_0\boldsymbol x_2}\Big|} {\Big\|\overrightarrow{\boldsymbol x_0\boldsymbol x_1}\Big\|} = \frac {|k| \cdot \Big|\boldsymbol w\cdot\overrightarrow{\boldsymbol x_0\boldsymbol x_2}\Big|} {|k|\cdot \boldsymbol w} = \frac {\Big|\boldsymbol w\cdot(\boldsymbol x_2 - \boldsymbol x_0)\Big|} {\boldsymbol w} = \frac {\Big|\boldsymbol w^\top\boldsymbol x_0 +b\Big|} {\boldsymbol w}.$

假设超平面可以对样本进行正确分类（假设没有样本点恰好落在超平面上），令

$\begin{cases} \boldsymbol w^\top\boldsymbol x + b \geqslant 1, & y_i = 1;\\ \boldsymbol w^\top\boldsymbol x + b \leqslant -1, & y_i = -1;\\ \end{cases}$

于是存在一些距离超平面最近的样本点使得上式中的某一个等号成立，这些样本点被称为支持向量 (Support Vector)。反过来讲，这些支持向量可以将分类超平面完全确定，如下图所示。考虑两个属于不同类别的支持向量，可以验证它们到超平面的距离之和为 $\displaystyle \gamma = \frac 2{\|\boldsymbol w\|}$ ，这被称为间隔 (Margin)。

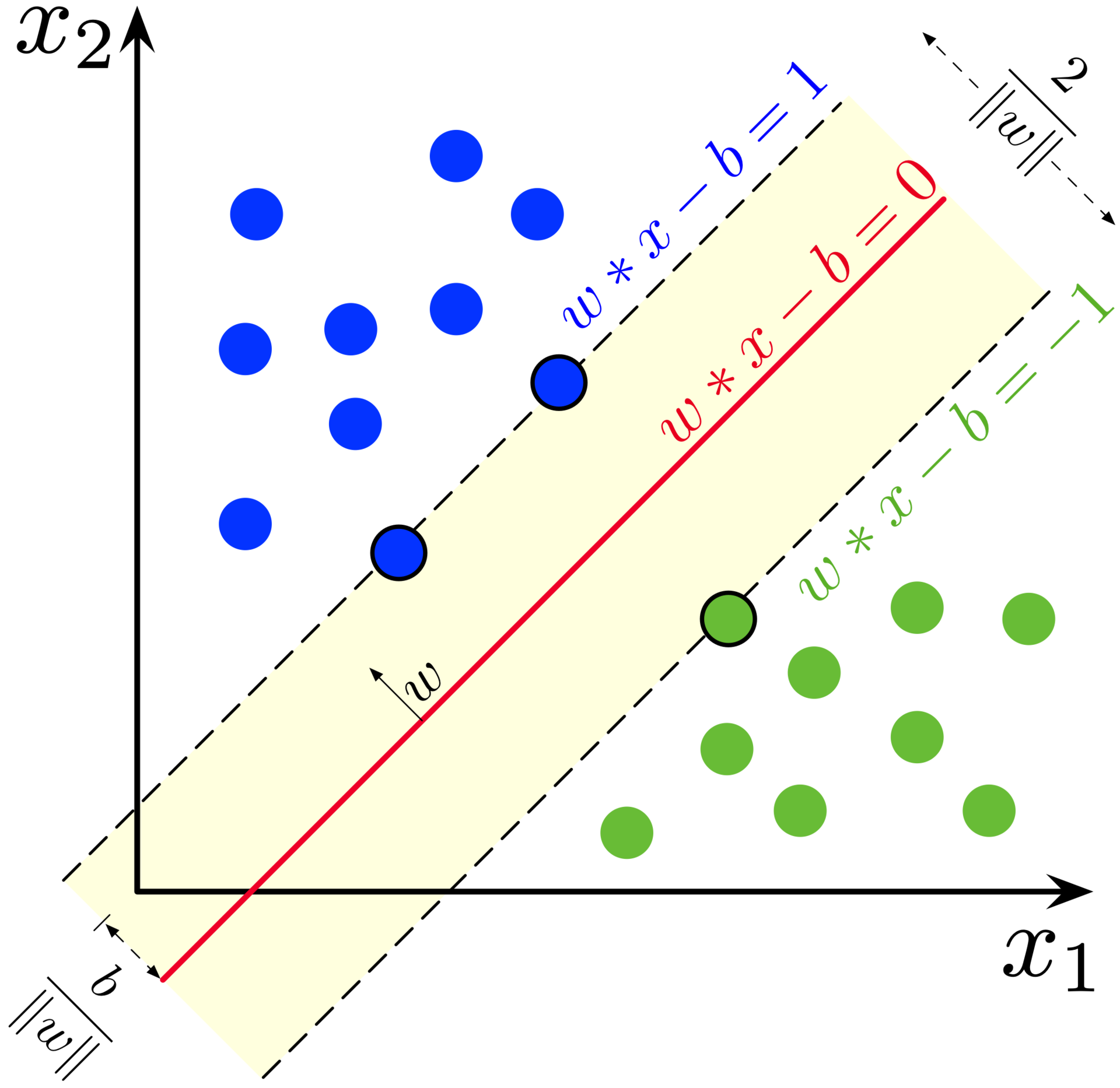
回顾上文中提到的我们的目标，是要找到泛化能力最好的那一个超平面，一种自然的思路就是让划分间隔越大越好，也即将两类分的越开越好。于是可以得到下面的优化问题

$\begin{align*} \mathop{\mathrm{maximize}}\limits_{\boldsymbol w, b} ~&~ \frac 2{\|\boldsymbol w\|} & \text{优化目标 (Optimization target)} \\ \text{subject to} ~&~ (\boldsymbol w^\top\boldsymbol x + b)y_i \geqslant 1, ~ i=1, ..., m & \text{约束条件 (Constraints)} \end{align*}$

显然这等价于最小化权重向量长度的平方，于是上述优化问题可以改写为

$\begin{align*} \mathop{\mathrm{maximize}}\limits_{\boldsymbol w, b} ~&~ f_0(\boldsymbol w, b) = \frac 12\|\boldsymbol w\|^2 \\ \text{subject to} ~&~ (\boldsymbol w^\top\boldsymbol x + b)y_i \geqslant 1, ~ i=1, ..., m \end{align*}\tag{$\star$}$

这就是支持向量机 (Support Vector Machine)模型

2 对偶问题 (Dual Problem)

2.1 Lagrange 对偶问题

TODO：对偶函数和对偶问题的直观意义

对于优化问题 $(\star)$ ，我们将每条约束与Lagrange乘子 $\alpha_i>0$ ，得到该问题的Lagrange函数

$L(\boldsymbol w, b, \boldsymbol \alpha) = \frac 12 \|\boldsymbol w\|^2 +\sum_{i=1}^m \alpha_i \Big( 1 - (\boldsymbol w^\top\boldsymbol x + b)y_i \Big)$

其中 $\boldsymbol \alpha$ 为所有Lagrange乘子堆叠形成的向量。注意到 $L$ 是一个关于 $\boldsymbol w$ 和 $b$ 的凸函数 (Convex Function)，将其分别对 $\boldsymbol w$ 和 $b$ 求偏导，并令偏导为零，可得

$\begin{align*} \boldsymbol w &= \sum_{i = 1}^m \alpha_iy_i\boldsymbol x_i\\ 0 &= \sum_{i = 1}^m \alpha_iy_i \end{align*}$

进而可以得到Lagrange对偶函数 (Lagrange Dual Function)

$g(\boldsymbol \alpha) = \inf_{\boldsymbol w, b} L(\boldsymbol w, b, \boldsymbol\alpha ) = \sum_{i=1}^m \alpha_i - \frac 12\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\boldsymbol x_i^\top\boldsymbol x_j.$

这样一来，原问题可以转化为最大Lagrange函数下界的对偶问题：

$\begin{align*} \mathop{\mathrm{maximize}}\limits_{\boldsymbol w, b} ~&~ g(\boldsymbol \alpha) \\ \text{subject to} ~&~ \sum_{i = 1}^m \alpha_iy_i = 0\\ ~&~ \alpha_i \geqslant 0, i=1,...,m \end{align*}$

通过求解最优的 $\alpha$ 后，将结果代入式中即可得到模型。

2.2 Karush-Kuhn-Tucker 条件

下面不加证明的引入两个定理：

定理对偶函数一定是凹函数 (Concave Function)

定理假设原问题最优解的目标函数值为 $p^\star$ ，则 $g(\cdot) \leqslant p^\star$

由于对偶函数是凹函数，于是对偶问题为凸优化问题，假设其最优解为 $\boldsymbol \alpha^\star$ ，对应的最优函数值为 $d^\star$

若 $d^\star \leqslant p^\star$ ，称为弱对偶 (Weak Duality)，并定义 $p^\star - d^\star$ 为对偶间隙 (Duality Gap)
若 $d^\star = p^\star$ ，称为强对偶 (Strong Duality)

若原优化问题和其对偶问题是强对偶关系，假设 $\boldsymbol w^\star, b^\star$ 和 $\boldsymbol \alpha^\star$ 分别为原问题和其对偶问题的最优解，则下面的条件称为 Karush-Kuhn-Tucker条件，简称KKT条件 (KKT Conditions) ：

$\left\{\begin{align*} \boldsymbol w^\star &= \sum_{i = 1}^m \alpha_i^\star y_i\boldsymbol x_i; & \text{稳定性条件 (Stationarity)}\\ 0 &= \sum_{i = 1}^m \alpha_i^\star y_i; & \text{稳定性条件 (Stationarity)}\\ \alpha_i^\star(y_i f(\boldsymbol x_i) - 1) &= 0; & \text{互补松弛条件 (Complementary Slackness)}\\ y_if(\boldsymbol x_i) - 1 &\geqslant 0; & \text{原问题可行性 (Primal Feasibility)} \\ \alpha_i &\geqslant 0. & \text{对偶问题可行性 (Dual Feasibility)}\\ \end{align*}\right.$

上面的互补松弛条件看起来不是很显然，这个条件表明，当 $\alpha_i^\star>0$ 时， $y_i f(\boldsymbol x_i) - 1 = 0$ ；当 $y_i f(\boldsymbol x_i) - 1< 0$ 时， $\alpha_i = 0$ 。现在给出证明：

$\begin{align*} f_0(\boldsymbol w^\star, b^\star) &= g(\boldsymbol \alpha^\star) & \text{对偶间隙为}0\\ &= \inf_{\boldsymbol w, b} \left\{ \frac 12 \|\boldsymbol w\|^2 +\sum_{i=1}^m \alpha_i^\star \Big( 1 - (\boldsymbol w^\top\boldsymbol x + b)y_i \Big) \right\} & \text{对偶函数定义}\\ &\leqslant \frac 12 \|\boldsymbol w^\star\|^2 +\sum_{i=1}^m \alpha_i^\star \Big( 1 - (\boldsymbol w^\star{}^\top\boldsymbol x + b^\star)y_i \Big) & \text{下确界}\\ &\leqslant \frac 12 \|\boldsymbol w^\star\|^2 & \text{对偶问题约束条件} \\ &= f_0(\boldsymbol w^\star, b^\star) \end{align*}$

注意到过程中的两个小于等于号只能取等号。于是 $\displaystyle \sum_{i=1}^m \alpha_i^\star \Big( 1 - (\boldsymbol w^\star{}^\top\boldsymbol x + b^\star)y_i \Big) = 0$ 。又因为求和式中的每一项不大于零，于是只有 $\displaystyle \alpha_i^\star \Big( 1 - (\boldsymbol w^\star{}^\top\boldsymbol x + b^\star)y_i \Big) = 0$ 。观察上述的KKT条件，不难发现只有数据中的支持向量才对模型做出了贡献。而其他大规模的样本并未真正参与。

2.2 对偶问题的求解

本节以SMO (Sequential Minimal Optimization) 为例讨论上述优化问题的求解方法。由于参数向量 $\boldsymbol\alpha$ 拥有多个分量，不妨考虑固定除两个分量 $\alpha_i$ 和 $\alpha_j$ 以外的其他所有分量后，优化受限制的目标函数直至收敛，则就是SMO的主要思路。

考虑随机选取的两个分量 $\alpha_i$ 和 $\alpha_j$ ，第二个稳定性条件可以简化为以下两项

$\begin{align*} \alpha_iy_i + \alpha_jy_j &= c,\\ \sum_{k \ne i,j} \alpha_ky_k + c&= 0. \end{align*}$

消去变量 $\alpha_j$ 后，原目标函数变成了单变量二次函数可以直接计算解析解。

在得到权重向量 $\boldsymbol w$ 之后，可以通过支持向量计算偏置 $b$ 。对于任何支持向量 $(\boldsymbol x_s, y_s)_{s \in S}$ ，有

$y_s \left( \sum_{i \in S} \alpha_iy_i \boldsymbol x_i^\top\boldsymbol x_s +b \right) = 1,$

于是考虑更加鲁棒的计算偏置方法

$b = \frac 1{|S|} \sum_{s \in S}\left( \frac 1{y_s} - \sum_{i \in S} \alpha_iy_i \boldsymbol x_i^\top\boldsymbol x_s\right).$

3 核函数 (Kernel Function)

3.1 核技巧 (Kernel Trick) 和核函数 (Kernel Function)

考虑使用线性模型分类异或问题的情形，不难发现一个线性分类器无法实现（当然，可以通过多个线性分类器实现）在本节我们考虑另一种方法。若可以找到一个映射$\phi$，将低维空间中的数据点嵌入高维空间，使得高维数据可以线性可分，就可以直接应用线性分类器的方法了。

将映射$\phi$应用于样本向量，在特征空间中的超平面就变为

$f(\boldsymbol x) = \boldsymbol w^\top \phi(\boldsymbol x) + b$

类似地，优化问题就变为

$\begin{align*} \mathop{\mathrm{maximize}}\limits_{\boldsymbol w, b} ~&~ f_0(\boldsymbol w, b) = \frac 12\|\boldsymbol w\|^2 \\ \text{subject to} ~&~ \left(\boldsymbol w^\top\phi(\boldsymbol x) + b\right)y_i \geqslant 1, ~ i=1, ..., m \end{align*}$

对偶问题就变为

$\begin{align*} \mathop{\mathrm{maximize}}\limits_{\boldsymbol w, b} ~&~ g(\boldsymbol \alpha) = \sum_{i=1}^m \alpha_i - \frac 12\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\phi(\boldsymbol x_i)^\top\phi(\boldsymbol x_j)\\ \text{subject to} ~&~ \sum_{i = 1}^m \alpha_iy_i = 0\\ ~&~ \alpha_i \geqslant 0, i=1,...,m \end{align*}$

考虑到高维或无穷维空间下计算向量内积较为困难，我们采用核技巧 (Kernel Trick)规避这一问题。定义函数

$\begin{align*} \kappa(\cdot, \cdot): \mathbb{R}^n\times \mathbb{R}^n &\rightarrow \mathbb{R}\\ (\boldsymbol x_i, \boldsymbol x_j) &\mapsto \langle \phi(\boldsymbol x_i),\phi(\boldsymbol x_j) \rangle = \phi(\boldsymbol x_i)^\top\phi(\boldsymbol x_j) \end{align*}$

这样对偶问题的目标函数可以简化为

$g(\boldsymbol \alpha) = \sum_{i=1}^m \alpha_i - \frac 12\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j \kappa(\boldsymbol x_i, \boldsymbol x_j)$

这里的$\kappa(\cdot, \cdot)$称为核函数 (Kernel Function)，求解后的线性分类器即为

$f(\boldsymbol x) = \boldsymbol w^\top \boldsymbol x +b = \sum_{i=1}^m \alpha_iy_i\kappa(\boldsymbol x, \boldsymbol x_i) +b,$

这被称为支持向量展式 (Support Vector Expansion)