1 The k-armed bandit problem, k臂赌博机

1 k-臂赌博机

Reinforcement Learning is to choose a series of actions to maximize the total expected reward, by trial and error, under uncertainty.

想象这样一个场景：我们到达一个之前没有去过的餐馆准备吃饭。我们准备从 $k$ 种菜里面选一种作为今天晚上的主菜。假设我们没有查阅其他人对这家餐馆的评论，那么，在我们之后多次光顾这家餐馆的情况下，我们如何做到在餐馆中的体验最好？（我们在此做一个极端假设，即我们中的每一个人对每一道菜的看法相同）

在上述场景中，我们称我们的选择为一个动作（action），记作 $a$ ；而在选择之后我们对菜的看法（如同美食节目中对菜打分）称为我们获得的奖励（reward），记作 $r$ 。由于餐馆厨师做菜水平在每一次并不是完全相同的，因此我们可以将选取特定菜所得的奖励的平均值记下来：

$q_*(a) := \mathbb E[R_t=r|A_t=a]$

然而真正的 $q_*(a)$ 是难以得知的。否则我们在首次来到这家餐馆时就可以直接选出我们认为最好的菜。因此，我们需要通过我们不断的尝试各种菜所得的奖励来估计真实的期望值：

$Q_t(a) := \frac{\displaystyle\sum_{i=1}^{t-1} R_i\cdot \mathbb 1_{A_i=a}}{\displaystyle\sum_{i=1}^{t-1} \mathbb 1_{A_i=a}}$

由大数定律，容易知道当分母趋于无穷大时， $Q_t(a) \rightarrow q_*(a)$ 。那么我们就可以很好的估计真实的奖励的期望值。那我们只要直接选择那个使得 $Q_t(a)$ 的值最大的那一个就好了……真的是这样吗？

2 探索与利用之两难

我们在餐厅点菜，我们可以一直点自己喜欢吃的那一道菜（事实上在现实中我就是这样做的），也可以试试其他的。我们称一直吃已知最好吃的菜这样的做法叫做利用（exploitation），或者说这种做法较为贪心（greedy）：

$A_t = \mathop{\mathrm{arg\max}}\limits_{a}~Q_t(a)$

我们也可以抛硬币，随便在这些菜里面选一道。这种做法被称为探索（exploration）。很显然这是我们的点菜策略的两个极端。而大多数情况下，我们更倾向于这样的选择：我们常常点自己最喜欢吃的菜，但因为吃的时间长了，想换换胃口，就随机试一试其他的菜。这就是接下来要介绍的 $\varepsilon$ -贪心方法（ $\varepsilon$ -greedy method）。我们选择一个 $0$ 到 $1$ 之间的数 $\varepsilon$ ，在我们每一次行动前，生成一个 $0$ 到 $1$ 之间的随机数，如果大于 $\varepsilon$ ，那就吃自己最喜欢吃的菜，反之，就试试其他的菜。这样一来，你作为这家餐馆的常客，久而久之你就能知道餐馆的每一道菜做的如何。当 $\varepsilon$ 很小的时候，你更倾向于保守，反之，你更倾向于试试其他的菜。

因为赌博有害家庭幸福，我在上面的叙述中将尽量避免直接提及它们。但是仔细思考可以发现，赌博机上的情况和上述情形极其相似。我们将对赌博机不加介绍的直接引入下一个概念——10-臂赌博机实验台。

3 10-臂赌博机实验台

对于上述的问题，我们通常用10-臂赌博机实验台（the 10-armed testbed）来测试我们目前并不能算智能的智能体（agent）。他是一个拥有大量 $k=10$ 的k-臂赌博机的集合。每一个10-臂赌博机的每一个 “臂” 所对应的奖励如下图所示

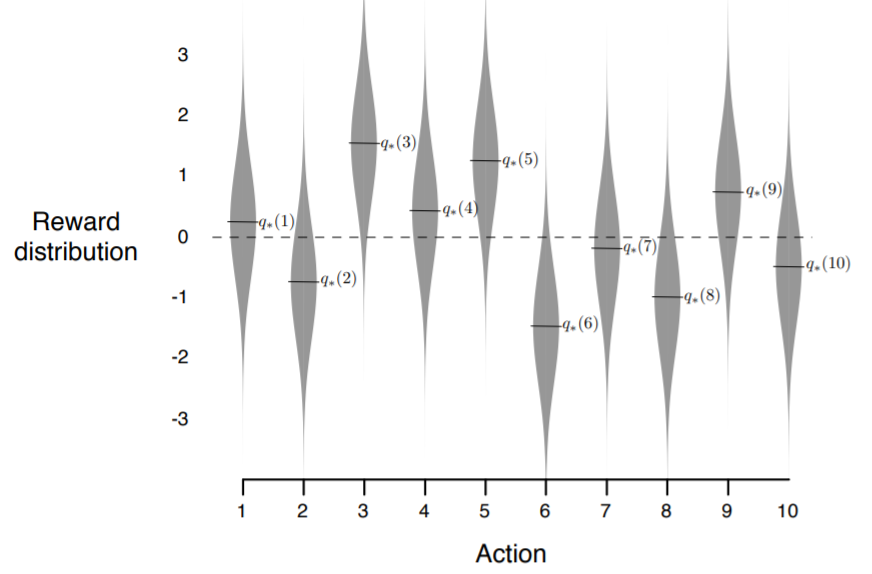
在上图中横坐标表示不同的选择（action），而纵坐标表示选择当前动作下对应奖励的概率分布。（一般地，每一个分布的标准差均为 $1$ ）图中表明的 $q_*(a)$ 即为每一个动作下对应的奖励的期望。而单独的一次动作所得的奖励只是在上述概率分布中按照其随机取得一个奖励。同时 $q_*(a)$ 本身也是来自于正态分布 $\mathcal N(0, 1)$ 。

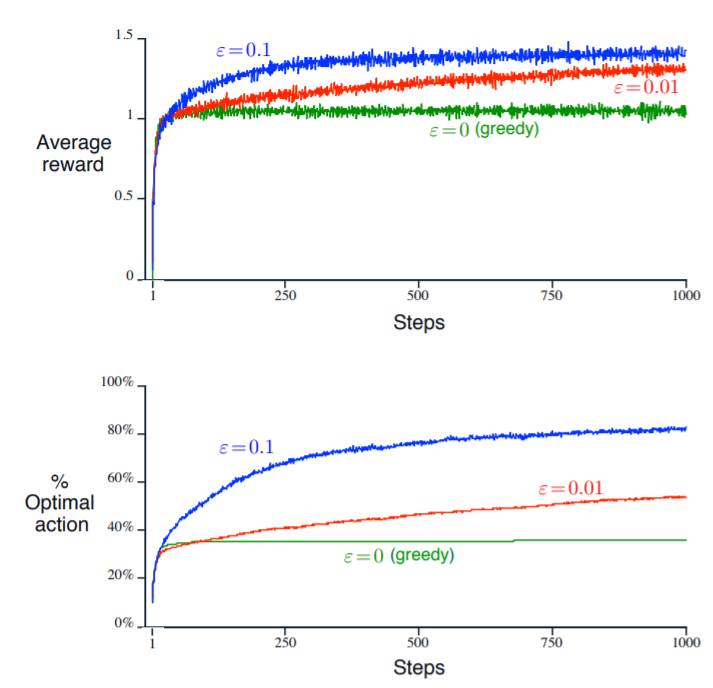
当我们拿着之前的贪心方法和 $\varepsilon$ 值不同的 $\varepsilon$ -贪心方法在实验台上测试，可以发现以下规律

贪心方法的平均奖励值在开始阶段上升的最快，但很快达到平台（plateau）
在 $250$ - $1000$ 迭代步数之内， $\varepsilon$ 值较大的平均奖励大

那么我们可以分析造成这种状况的原因。贪心方法可以很快地找到使得估计均值最大的那一个动作。从此以后难以再改变。因此在达到高点以后平均奖励不在上升。好比选到一款好菜，就吃定了它，自然不在意其他的菜怎么样，即使存在一道菜甚至比你现在认为的最好吃的菜要好吃得多。 $\varepsilon$ 值较小的方法对应的平均奖励上升的比 $\varepsilon$ 值较大的方法慢，这也是很好解释的，因为它探索的不够多。

4 增量实现

我们在计算价值函数的近似时需要用到平均数，而我们在迭代过程中需要不断更新这一个平均数。显然我们如果每次都去重新计算这一个平均数的话显得很麻烦。于是我们可以采取如下的方法：

$\mu_{n+1} = \frac 1{n+1}\sum_{i = 1}^{n+1} x_i = \frac 1{n+1}\left( x_{n+1} + \sum_{i=1}^nx_i \right) = \frac 1{n+1}x_{n+1} + \frac n{n+1}\mu_n = \mu_n + \frac{x_{n+1 - \mu_n}}{n+1}$

于是 $Q_t(a)$ 的更新过程可以表示为

$Q_{n+1}(a) = Q_n(a) + \mathbb 1_{A_n=a} \left(\frac{R_{n} - Q_{n+1}(a)}{n+1}\right)$

5 Softmax 选择策略

假设我们获取了所有状态对应的 $Q$ 函数的集合（注意是估计值而不是真实值）我们可以这样定义决策时选择动作：

$\mathrm {Pr}[A_t = a] = \frac{e^{Q_{t} (a) / \tau}}{\sum\limits_{a}e^{Q_t(a) / \tau}}$

这样我们就构造了一个在动作空间 $\mathscr A$ 上的概率分布。只要在选取时按照这样的概率分布来选择动作即可。我们采用Python的numpy库可以对此进行方便的实现，从而使得上述的k臂赌博机问题有更快的收敛速度

import numpy as np
import matplotlib.pyplot as plt


def get_reward(prob: float) -> float:
	reward = prob * 10 + 1 * np.random.randn()  # get reward from normal siatribution
	return reward if 1 <= reward <= 10 else 0 if reward < 0 else 10


def update_record(record: np.array, action: int, reward: float) -> np.array:
	new_r = (record[action, 0] * record[action, 1] + reward) / (record[action, 0] + 1)
	record[action, 0] += 1
	record[action, 1] = new_r
	return record


def softmax(array: np.array, tau: float = 1.15) -> np.array:
	res = np.exp(array / tau) / np.sum(np.exp(array / tau))
	return res


def main()
    # Initialization
    n = 10
    probs = np.random.rand(n)
    record = np.zeros((n, 2))
    fig, ax = plt.subplots(1, 1)
    ax.set_xlabel("Plays")
    ax.set_ylabel("Avg_Reward")
    fig.set_size_inches(9, 5)
    rewards = [0]

    # Begin Iteriation
    for i in range(500):
        p = softmax(record[:, 1])

        #! Choose action accroding to the probability distribution
        choice = np.random.choice(np.arange(n), p=p)
        r = get_reward(probs[choice])

        record = update_record(record, choice, r)
        mean_reward = ((i + 1) * rewards[-1] + r) / (i + 2)
        rewards.append(mean_reward)

    # Plot the results
    ax.scatter(np.arange(len(rewards)), rewards)
    plt.show()
    
    return 0

if __name__ == "__main__":
	main()